题目内容
已知椭圆E：
+
=1过点A（-1，0）和点B（1，0），其中一个焦点与抛物线y=
x2的焦点重合，C为E上异于顶点的任一点．
（Ⅰ）求椭圆E的方程；
（Ⅱ）若椭圆E所在平面上的两点M，G同时满足：①
+
+
=
；②|
|=|
|=|
|．试问直线MG的斜率是否为定值，若为定值求出该定值；若不为定值，请说明理由．
| x2 |
| m2 |
| y2 |
| n2 |
| ||
| 8 |
（Ⅰ）求椭圆E的方程；
（Ⅱ）若椭圆E所在平面上的两点M，G同时满足：①
. |
| GA |
. |
| GB |
. |
| GC |
. |
| 0 |
. |
| MA |
. |
| MB |
. |
| MC |
考点：圆锥曲线的综合
专题：向量与圆锥曲线
分析：（Ⅰ）化抛物线方程为标准式，求出焦点坐标，由题意得到椭圆的长半轴，再由椭圆一个焦点与抛物线焦点重合得到椭圆的半焦距，结合隐含条件得b，则椭圆方程可求；
（Ⅱ）设出C点坐标，由①②可知G为三角形重心，M为三角形外心，把G点坐标用C点坐标表示，再设出M点坐标，由|
|=|
|得到B，C坐标的关系，结合C点在椭圆上可得M的坐标，则MG所在直线斜率可求．
（Ⅱ）设出C点坐标，由①②可知G为三角形重心，M为三角形外心，把G点坐标用C点坐标表示，再设出M点坐标，由|
. |
| MA |
. |
| MC |
解答：
解：（Ⅰ）由y=
x2，得x2=4
y，
∴抛物线的焦点坐标为(0，
)，
由题意知m2=1，
又c=
，
∴n2=m2+(
)2=1+2=3，
∴椭圆E的方程为x2+
=1；
（Ⅱ）设C（x0，y0），
由
+
+
=
可知G为△ABC的重心，
则G(
，
)．
由|
|=|
|=|
|知M为△ABC的外心，
故设M（0，y1），
由|
|=|
|，得1+y12=x02+(y0-y1)2，
整理得：x02+y02-2y0y1=1．
又x02+
=1，
∴
y02-2y0y1=0．
∴y0=3y1，
则M（0，
）．
∴kMG=0．
即直线MG的斜率是定值0．
| ||
| 8 |
| 2 |
∴抛物线的焦点坐标为(0，
| 2 |
由题意知m2=1，
又c=
| 2 |
∴n2=m2+(
| 2 |
∴椭圆E的方程为x2+
| y2 |
| 3 |
（Ⅱ）设C（x0，y0），
由
. |
| GA |
. |
| GB |
. |
| GC |
. |
| 0 |
则G(
| x0 |
| 3 |
| y0 |
| 3 |
由|
. |
| MA |
. |
| MB |
. |
| MC |
故设M（0，y1），
由|
. |
| MA |
. |
| MC |
整理得：x02+y02-2y0y1=1．
又x02+
| y02 |
| 3 |
∴
| 2 |
| 3 |
∴y0=3y1，
则M（0，
| y0 |
| 3 |
∴kMG=0．
即直线MG的斜率是定值0．
点评：本题是圆锥曲线的综合题，考查椭圆方程的求法，考查了由向量关系判断三角形的重心和外心，体现了整体代换思想方法，是压轴题．
练习册系列答案
相关题目
“p∧q是假命题”是“￢p为真命题”的（ ）
| A、必要不充分条件 |
| B、充分不必要条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
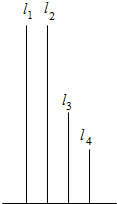
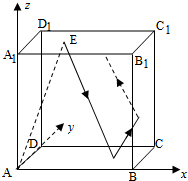如图，在长方体ABCD-A1B1C1D1中，AB=11，AD=7，AA1=12．一质点从顶点A射向点E（4，3，12），遇长方体的面反射（反射服从光的反射原理），将第i-1次到第i次反射点之间的线段记为li（i=2，3，4），l1=AE，将线段l1，l2，l3，l4竖直放置在同一水平线上，则大致的图形是（ ）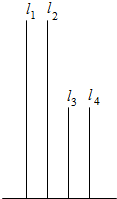
如图，在△ABC中，已知D为BC边上的中点，且cosB=