题目内容
设sinθ=
(m>0),则cos(θ+
)的取值范围是( )
| m2+1 |
| 4m |
| π |
| 6 |
A、[-1,
| ||||||
B、[-1,
| ||||||
C、[-
| ||||||
D、[-
|
考点:运用诱导公式化简求值
专题:三角函数的求值
分析:已知等式右边变形后,利用基本不等式求出sinθ范围,进而确定出θ的范围,即θ+
的范围,利用余弦函数性质即可求出cos(θ+
)的取值范围.
| π |
| 6 |
| π |
| 6 |
解答:
解:∵sinθ=
(m>0)=
+
≥
,
∴
+2kπ≤θ≤
+2kπ,k∈Z,即
+2kπ≤θ+
≤π+2kπ,k∈Z,
∴-1≤cos(θ+
)≤
,
则cos(θ+
)的取值范围是[-1,
].
故选:A.
| m2+1 |
| 4m |
| m |
| 4 |
| 1 |
| 4m |
| 1 |
| 2 |
∴
| π |
| 6 |
| 5π |
| 6 |
| π |
| 3 |
| π |
| 6 |
∴-1≤cos(θ+
| π |
| 6 |
| 1 |
| 2 |
则cos(θ+
| π |
| 6 |
| 1 |
| 2 |
故选:A.
点评:此题考查了运用诱导公式化简求值,以及正弦、余弦函数的性质,熟练掌握三角函数性质是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
若(x2-
)9(a∈R)的展开式中x9项的系数为-
,则函数f(x)=sinx与直线x=a、x=-a及x轴围成的封闭图形的面积为( )
| 1 |
| ax |
| 21 |
| 2 |
| A、2-2cos2 |
| B、4-2cos1 |
| C、0 |
| D、2+2cos2 |
设a=(
)-
,b=log
3,c=log
,则a,b,c的大小关系是( )
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| A、a>b>c |
| B、b>a>c |
| C、c>a>b |
| D、a>c>b |
已知
=1-i,其中x,y∈R,i为虚数单位,则x+yi=( )
| x |
| 1+yi |
| A、1+2i | B、1-2i |
| C、2+i | D、2-i |
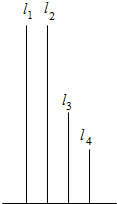
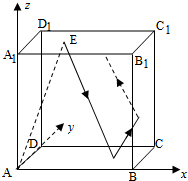 如图,在长方体ABCD-A1B1C1D1中,AB=11,AD=7,AA1=12.一质点从顶点A射向点E(4,3,12),遇长方体的面反射(反射服从光的反射原理),将第i-1次到第i次反射点之间的线段记为li(i=2,3,4),l1=AE,将线段l1,l2,l3,l4竖直放置在同一水平线上,则大致的图形是( )
如图,在长方体ABCD-A1B1C1D1中,AB=11,AD=7,AA1=12.一质点从顶点A射向点E(4,3,12),遇长方体的面反射(反射服从光的反射原理),将第i-1次到第i次反射点之间的线段记为li(i=2,3,4),l1=AE,将线段l1,l2,l3,l4竖直放置在同一水平线上,则大致的图形是( )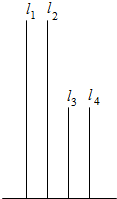


 如图,在△ABC中,已知D为BC边上的中点,且cosB=
如图,在△ABC中,已知D为BC边上的中点,且cosB=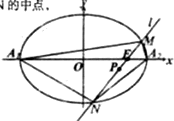 已知椭圆C:
已知椭圆C: