题目内容
（1）已知圆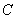
的参数方程为
（
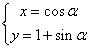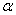为参数），以原点为极点，
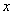轴正半轴为极轴建立极坐标系，直线
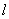的极坐标方程为
,(
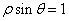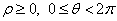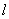)则直线与圆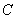的交点的极坐标为______________．
；
练习册系列答案
优百分课时互动系列答案
相关题目
优百分课时互动系列答案题目内容
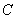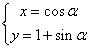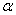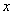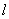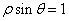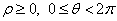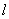（1）已知圆的参数方程为（为参数），以原点为极点，轴正半轴为极轴建立极坐标系，直线的极坐标方程为,()则直线与圆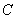的交点的极坐标为______________．
；
优百分课时互动系列答案
C．98 D．49
的离心率与等轴双曲线的离心率互为倒数，直线l: x－y＋
＝0与以原点为圆心，以椭圆C的短半轴长为半径的圆相切。
则f′（x）
的解集为 （ ）
B．（-1,0）
C．
D．
；
求
的值；
求实数
的值.
在x=2处切线方程的斜率是（ ）
的离心率为
，左顶点为（-1，0）。
上，求m的值和线段AB的长。
。
，求
在[－2，2] 上的最大值和最小值；