题目内容
已知椭圆C：
的离心率与等轴双曲线的离心率互为倒数，直线l: x－y＋
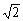＝0与以原点为圆心，以椭圆C的短半轴长为半径的圆相切。
（1）求椭圆C的方程；
（2）设M是椭圆的上顶点，过点M分别作直线MA, MB交椭圆于A, B两点，设两直线的斜率分别为k1, k2, 且k1＋k2＝2，证明：直线AB过定点(―1, ―1).
解：（1）由题意得
，
即
，解得
故椭圆C的方程为
（2）当直线AB的斜率不存在时，设A
,则B
，由k1＋k2＝2得
，得
当直线AB的斜率存在时，设AB的方程为y=kx+b（
）,
,
得
，
即
由，
即
故直线AB过定点(―1, ―1).
练习册系列答案
孟建平小学滚动测试系列答案
黄冈天天练口算题卡系列答案
相关题目
)的图像可由曲线y＝1＋cos2x向左平移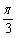
个单位得到；②函数y＝sin(x＋
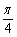)＋cos(x＋
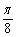是曲线y＝sin(2x＋
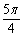)的一条对称轴；④函数y＝2sin2(x＋
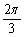)＋sin(wx－
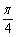)上单调递增 B．f(x)在(0, 
)上单调递增 D．f(x)在(0, 
为参数），则直线L的倾斜角的余弦值为（ ）
B．
C．
D．
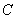的参数方程为
（
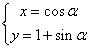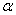为参数），以原点为极点，
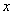轴正半轴为极轴建立极坐标系，直线
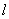的极坐标方程为
,(
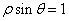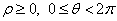)则直线
的实根个数是（ ）
的图象向左平移
个单位，得到函数
的图象，则
是 （ ） 
B．cosx C．sinx D．2cosx