题目内容
设椭圆Γ1的中心和抛物线Γ2的顶点均为原点O,Γ1、Γ2的焦点均在x轴上,过Γ2的焦点F作直线l,与Γ2交于A、B两点,在Γ1、Γ2上各取两个点,将其坐标记录于下表中:
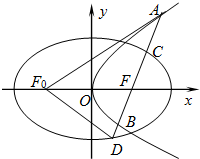
(1)求Γ1,Γ2的标准方程;
(2)若l与Γ1交于C、D两点,F0为Γ1的左焦点,求
的最小值.
| x | 3 | -2 | 4 |
| ||||||
| y | -2
| 0 | -4 | -
|

(1)求Γ1,Γ2的标准方程;
(2)若l与Γ1交于C、D两点,F0为Γ1的左焦点,求
| S△F0AB |
| S△F0CD |
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(1)由题意知(-2,0),(
,-
)在椭圆上,(3,-2
),(4,-4)在抛物线上,由此能求出椭圆Γ1方程和抛物线Γ2方程.
(2)设F0到直线l的距离为d,
=
=
,当直线l的斜率存在时,
>
;当直线l的斜率不存在时,
=
,由此能求出
的最小值.
| 3 |
| ||
| 2 |
| 3 |
(2)设F0到直线l的距离为d,
| S△F0AB |
| S△F0CD |
| ||
|
| |AB| |
| |CD| |
| S△F0AB |
| S△F0CD |
| 4 |
| 3 |
| S△F1AB |
| S△F1CD |
| 4 |
| 3 |
| S△F0AB |
| S△F0CD |
解答:
解:(1)由题意知(-2,0),(
,-
)在椭圆上,
(3,-2
),(4,-4)在抛物线上,…(2分)
设椭圆Γ1方程为
+
=1(a>b>0),
则
,解得a=2,b=
,
∴椭圆Γ1的方程为
+
=1.
设抛物线Γ2方程为y2=2py(p>0),
则(-4)2=2P×4,解得p=2,
∴抛物线Γ2方程为y2=4x.…(6分)
(2)设F0到直线l的距离为d,
=
=
.…(7分)
F(1,0)是抛物线的焦点,也是椭圆的右焦点,
①当直线l的斜率存在时,
设l:y=k(x-1),设A(x1,y1),B(x2,y2),C(x3 ,y3),D(x4,y4),
联立方程
,得k2x2-(2k2+4)x+k2=0,
k≠0时,△>0恒成立.
|AB|=
=
=
,…(9分)
联立方程
,得(3+4k2)x2-8k2x+4k2-12=0,△>0恒成立.
|CD|=
=
=
,
∴
=
=
=
+
>
.…(11分)
②当直线l的斜率不存在时,l:x=1,
此时,|AB|=4,|CD|=3,
=
.…(12分)
∴
的最小值为
.…(13分)
| 3 |
| ||
| 2 |
(3,-2
| 3 |
设椭圆Γ1方程为
| x2 |
| a2 |
| y2 |
| b2 |
则
|
| 3 |
∴椭圆Γ1的方程为
| x2 |
| 4 |
| y2 |
| 3 |
设抛物线Γ2方程为y2=2py(p>0),
则(-4)2=2P×4,解得p=2,
∴抛物线Γ2方程为y2=4x.…(6分)
(2)设F0到直线l的距离为d,
| S△F0AB |
| S△F0CD |
| ||
|
| |AB| |
| |CD| |
F(1,0)是抛物线的焦点,也是椭圆的右焦点,
①当直线l的斜率存在时,
设l:y=k(x-1),设A(x1,y1),B(x2,y2),C(x3 ,y3),D(x4,y4),
联立方程
|
k≠0时,△>0恒成立.
|AB|=
| (1+k2)(x2-x1)2 |
(1+k2)•
|
| 4(1+k2) |
| k2 |
联立方程
|
|CD|=
| (1+k2)(x3-x4)2 |
(1+k2)•
|
| 12(1+k2) |
| 3+4k2 |
∴
| S△F0AB |
| S△F0CD |
| ||
|
| 3+4k2 |
| 3k2 |
| 1 |
| k2 |
| 4 |
| 3 |
| 4 |
| 3 |
②当直线l的斜率不存在时,l:x=1,
此时,|AB|=4,|CD|=3,
| S△F1AB |
| S△F1CD |
| 4 |
| 3 |
∴
| S△F0AB |
| S△F0CD |
| 4 |
| 3 |
点评:本题考查椭圆方程和抛物线方程的求法,考查两个三角形面积比值的最小值的求法,解题时要认真审题,注意分类讨论思想的合理运用.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
设t是实数,i是虚数单位,且
+
是实数,则t=( )
| t |
| 1+i |
| 1-i |
| 2 |
| A、-1 | B、1 | C、0 | D、2 |
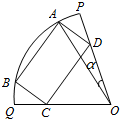 已知OPQ是半径为1,圆心角为2θ(θ为定值)的扇形,A是扇形弧上的动点,四边形ABCD是扇形内的内接矩形,记∠AOP=α(0<α<θ).
已知OPQ是半径为1,圆心角为2θ(θ为定值)的扇形,A是扇形弧上的动点,四边形ABCD是扇形内的内接矩形,记∠AOP=α(0<α<θ). 设四边形ABCD内接于圆O,其对边AD与BC的延长线交于圆O外一点E,自E引一直线平行于AC,交BD延长线于点M,自M引MT切圆O于T点,则MT=ME.
设四边形ABCD内接于圆O,其对边AD与BC的延长线交于圆O外一点E,自E引一直线平行于AC,交BD延长线于点M,自M引MT切圆O于T点,则MT=ME.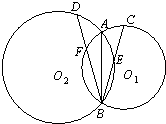 如图,假设两圆O1和O2交于A、B,⊙O1的弦BC交⊙O2于E,⊙O2的弦BD交⊙O1于F,证明:
如图,假设两圆O1和O2交于A、B,⊙O1的弦BC交⊙O2于E,⊙O2的弦BD交⊙O1于F,证明: