题目内容
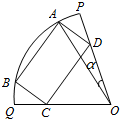 已知OPQ是半径为1,圆心角为2θ(θ为定值)的扇形,A是扇形弧上的动点,四边形ABCD是扇形内的内接矩形,记∠AOP=α(0<α<θ).
已知OPQ是半径为1,圆心角为2θ(θ为定值)的扇形,A是扇形弧上的动点,四边形ABCD是扇形内的内接矩形,记∠AOP=α(0<α<θ).(1)用α表示矩形ABCD的面积S;
(2)若θ=
| π |
| 6 |
考点:三角函数的最值,弧度制的应用
专题:三角函数的图像与性质
分析:(1)由题意可得△COD为等边三角形,求得AB,在△OAB中,利用正弦定理求得AD.可得矩形ABCD的面积S=f(α).
(2)由(1)可得S=f(α).再由 0<α<
,根据正弦函数的定义域和值域求得S=f(α)的最大值.
(2)由(1)可得S=f(α).再由 0<α<
| π |
| 6 |
解答:
 解:(1)由题意可得AD∥OE∥CB,
解:(1)由题意可得AD∥OE∥CB,
∴∠POE=∠PDA=θ,∴∠ODC=
-θ=∠DCO,∠BOA=2θ-2α,△COD为等腰三角形.
故AB=2sin(θ-α),
再由∠ADO=
+
-θ=π-θ,
△OAD中,利用正弦定理可得
=
,
化简可得AD=
.
故矩形ABCD的面积S=f(α)=AB•AD=
.
(2)θ=
,由(1)可得S=f(α)=
=2sinαcosα-2
sin2α=sin2α+
cos2α-
=2(
sin2α+
cos2α)-
=2sin(2α+
)-
.
再由 0<α<
可得
<2α+
<
,
故当 2α+
=
,即当α=
时,S=f(α)取得最大值为2-
.
 解:(1)由题意可得AD∥OE∥CB,
解:(1)由题意可得AD∥OE∥CB,∴∠POE=∠PDA=θ,∴∠ODC=
| π |
| 2 |
故AB=2sin(θ-α),
再由∠ADO=
| π |
| 2 |
| π |
| 2 |
△OAD中,利用正弦定理可得
| AD |
| sinα |
| 0A |
| sin(π-θ) |
化简可得AD=
| sinα |
| sinθ |
故矩形ABCD的面积S=f(α)=AB•AD=
| 2sin(θ-α)sinα |
| sinθ |
(2)θ=
| π |
| 6 |
2sin(
| ||
sin
|
| 3 |
| 3 |
| 3 |
=2(
| 1 |
| 2 |
| ||
| 2 |
| 3 |
| π |
| 3 |
| 3 |
再由 0<α<
| π |
| 6 |
| π |
| 3 |
| π |
| 3 |
| 2π |
| 3 |
故当 2α+
| π |
| 3 |
| π |
| 2 |
| π |
| 12 |
| 3 |
点评:本题主要考查直角三角形中的边角关系、两角和差的三角公式、正弦函数的定义域和值域,正弦定理的应用,属于中档题.

练习册系列答案
相关题目
三角形ABC中,∠C=90°,AB=2,AC=1,若
=
,则
•
=( )
| AD |
| 3 |
| 2 |
| AB |
| CD |
| CB |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
在△ABC中,A,B,C所对边分别为a,b,c,则下列各式中一定成立的是( )
A、
| ||||
B、
| ||||
| C、asinB=bcosA | ||||
| D、a=2RcosA |
定义:称
为n个正数p1,p2,…,pn的“均倒数”,若数列{an}的前n项的“均倒数”为
,则数列{an}的通项公式为( )
| n |
| p1+p2+…+pn |
| 1 |
| 2n-1 |
| A、2n-1 | B、4n-3 |
| C、4n-1 | D、4n-5 |
 如图,正六边形ABCDEF中,已知
如图,正六边形ABCDEF中,已知