题目内容
函数f（x）=（x-2）ln（x2-4x+4）-（x-2）ln4的零点个数为（ ）
| A、3 | B、2 | C、1 | D、0 |
考点：函数零点的判定定理
专题：函数的性质及应用
分析：令函数f（x）=（x-2）ln（x2-4x+4）-（x-2）ln4=0，把x的值直接解出即可．
解答：
解；令函数f（x）=（x-2）ln（x2-4x+4）-（x-2）ln4=0，
∴（x-2）ln
=0，
∴x-2=0，①
或
=1②
解①得：x=2，
解②得：x=0，x=4．
∴所求零点的个数为3个，
故选：A．
∴（x-2）ln
| x2-4x+4 |
| 4 |
∴x-2=0，①
或
| x2-4x+4 |
| 4 |
解①得：x=2，
解②得：x=0，x=4．
∴所求零点的个数为3个，
故选：A．
点评：本题考察了函数零点的判定定理，本题是一道基础题，解题时防止出错．
练习册系列答案
相关题目
执行如图所示的程序框图，当输入的x=9时，则输出的k=（ ）
| A、2 | B、3 | C、4 | D、5 |
已知圆的方程是（x-2）2+（y-3）2=4，则点P（-3，-2）满足（ ）
| A、是圆心 | B、在圆上 |
| C、在圆内 | D、在圆外 |
对于二项式（1-x）1999，有下列四个命题正确的是（ ）
A、展开式中T1000=C
| ||
| B、展开式中非常数项系数和是1 | ||
| C、展开式中系数最大的项是第1000项和第1001项 | ||
| D、当x=2000时，（1-x）1999除以2000的余数是1 |
已知a，b，c∈R，a+b+c=0，abc＞0，T=
+
+
，则（ ）
| 1 |
| a |
| 1 |
| b |
| 1 |
| c |
| A、T＞0 | B、T＜0 |
| C、T=0 | D、T≥0 |
已知sin（
+α）=
，则cos（
+α）的值为（ ）
| π |
| 3 |
| 4 |
| 5 |
| 5π |
| 6 |
A、-
| ||
B、
| ||
C、-
| ||
D、
|
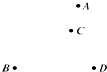如图A、B、C、D是某油田的四口油井，计划建三条路，将这四口油井连结起来（每条路只连结两口油井），那么不同的建路方案有（ ）| A、12种 | B、14种 |
| C、16种 | D、18种 |