题目内容
已知cosα=-
,且tanα<0,则sin2α的值等于( )
| ||
| 3 |
A、
| ||||
B、
| ||||
C、-
| ||||
D、-
|
考点:二倍角的正弦
专题:三角函数的求值
分析:首先,结合条件得到sinα>0,进一步求解sinα的值,然后,借助于二倍角的正弦公式进行求解即可.
解答:
解:∵cosα<0,且tanα<0,
∴sinα>0,
∵cosα=-
,
∴sinα=
=
=
,
∴sin2α=2sinαcosα
=2×
×(-
)
=-
,
故选:C.
∴sinα>0,
∵cosα=-
| ||
| 3 |
∴sinα=
| 1-cos2α |
1-
|
| ||
| 3 |
∴sin2α=2sinαcosα
=2×
| ||
| 3 |
| ||
| 3 |
=-
2
| ||
| 3 |
故选:C.
点评:本题考查了三角函数的符号,三角函数基本关系式,二倍角公式等知识点,属于中档题.

练习册系列答案
相关题目
如果-1,m、n、p、-16成等比数列,那么( )
| A、n=-4,mp=-16 |
| B、n=-4,mp=16 |
| C、n=4,mp=16 |
| D、n=4,mp=-16 |
设复数ω1=-
+
i,ω2=cos
+isin
,若z=ω1•ω2,则复数z的虚部为( )
| 1 |
| 2 |
| ||
| 2 |
| π |
| 12 |
| π |
| 12 |
A、-
| ||||
B、
| ||||
C、-
| ||||
D、
|
执行如图所示的程序框图,当输入的x=9时,则输出的k=( )


| A、2 | B、3 | C、4 | D、5 |
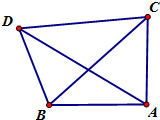 A,B两地相距200m,且A地在B地的正东方.一人在A地测得建筑C在正北方,建筑D在北偏西60°;在B地测得建筑C在北偏东45°,建筑D在北偏西15°,则两建筑C和D之间的距离为( )
A,B两地相距200m,且A地在B地的正东方.一人在A地测得建筑C在正北方,建筑D在北偏西60°;在B地测得建筑C在北偏东45°,建筑D在北偏西15°,则两建筑C和D之间的距离为( )A、200
| ||
B、100
| ||
C、100
| ||
D、100(
|
对于二项式(1-x)1999,有下列四个命题正确的是( )
A、展开式中T1000=C
| ||
| B、展开式中非常数项系数和是1 | ||
| C、展开式中系数最大的项是第1000项和第1001项 | ||
| D、当x=2000时,(1-x)1999除以2000的余数是1 |
在复平面上复数i,1,4+2i所对应的点分别是A、B、C,则平行四边形ABCD的对角线BD的长为( )
| A、5 | ||
B、
| ||
C、
| ||
D、
|