题目内容
11.已知函数f(x)=2cosx(sinx-cosx)+m(m∈R),将y=f(x)的图象向左平移$\frac{π}{4}$个单位后得到y=g(x)的图象,且y=g(x)在区间$[{0,\frac{π}{4}}]$内的最大值为$\sqrt{2}$.(1)求实数m的值;
(2)求函数y=g(x)与直线y=1相邻交点间距离的最小值.
分析 (1)运用二倍角公式化简f(x)的解析式,再由平移变换可得g(x)的表达式,结合正弦函数的最值,即可得到所求m的值;
(2)解方程$\sqrt{2}sin(2x+\frac{π}{4})=1$,即可得到所求相邻交点间距离的最小值.
解答 解:(1)f(x)=2cosx(sinx-cosx)+m=sin2x-cos2x-1+m=$\sqrt{2}sin(2x-\frac{π}{4})-1+m$,
所以,g(x)=$\sqrt{2}sin(2x+\frac{π}{4})-1+m$,2分
∵x∈$[{0,\frac{π}{4}}]$,∴$2x+\frac{π}{4}∈[{\frac{π}{4},\frac{3π}{4}}]$,
∴当$2x+\frac{π}{4}=\frac{π}{2}$时,即$x=\frac{π}{8}$时,函数g(x)取得最大值$\sqrt{2}-1+m=\sqrt{2}$,
则m=1. 5分
(2)∴g(x)=$\sqrt{2}sin(2x+\frac{π}{4})=1$,
$sin(2x+\frac{π}{4})=\frac{{\sqrt{2}}}{2}$,$2x+\frac{π}{4}=2kπ+\frac{π}{4}$或$2x+\frac{π}{4}=2kπ+\frac{3π}{4}$,7分
解得x1=k1π或${x_2}={k_2}π+\frac{π}{4}$,k1,k2∈Z.8分
因为$|{{x_1}-{x_2}}|=|{({k_1}-{k_2})π-\frac{π}{4}}|≥\frac{π}{4}$,当k1=k2时取等号,
∴相邻交点间距离的最小值是$\frac{π}{4}$.10分.
点评 本题考查三角函数的恒等变换,考查正弦函数的图象和性质,考查化简整理的运算能力,属于中档题.

 新思维寒假作业系列答案
新思维寒假作业系列答案| A. | $\frac{1}{a}<\frac{1}{b}$ | B. | $0<\frac{a}{b}<1$ | C. | ab>b2 | D. | $\frac{b}{a}>\frac{a}{b}$ |
| A. | f′(x)=2e2x | B. | f′(x)=$\frac{(2x-1){e}^{2x}}{{x}^{2}}$ | C. | f′(x)=$\frac{2{e}^{2x}}{x}$ | D. | f′(x)=$\frac{(x-1){e}^{2x}}{{x}^{2}}$ |
| A. | 9:4 | B. | 4:3 | C. | 3:1 | D. | 3:2 |
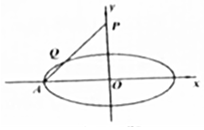 如图,过椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左顶点A作直线交y轴于点P,交椭圆于点Q,若△AOP是等腰三角形,且$\overrightarrow{PQ}$=2$\overrightarrow{QA}$,则椭圆的离心率是$\frac{2\sqrt{5}}{5}$.
如图,过椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左顶点A作直线交y轴于点P,交椭圆于点Q,若△AOP是等腰三角形,且$\overrightarrow{PQ}$=2$\overrightarrow{QA}$,则椭圆的离心率是$\frac{2\sqrt{5}}{5}$.