题目内容
16．已知定义在R上的函数f（x）为单调函数，且对任意x∈R，恒有f（f（x）-2x）=-$\frac{1}{2}$，若f（x0）=0，则x0的值是（ ）| A． | -1 | B． | 0 | C． | 1 | D． | 2 |
分析 运用换元法转化求解a=f（x）-2x，f（a）=-$\frac{1}{2}$，2a+a=-$\frac{1}{2}$，求出a的值即可求出f（x）的解析式，再求出零点即可．
解答 解：f（f（x）-2x）=-$\frac{1}{2}$，
设a=f（x）-2x，
则f（x）=2x+a，
∵f（a）=-$\frac{1}{2}$，
∴2a+a=-$\frac{1}{2}$，
解得：a=-1
所以f（x）=2x-1，
当f（x）=0时，x=0，
函数f（x）的零点是x0=0，
故选：B．
点评 本题综合考查了函数的概念，性质，思维能力强，要有一定的变换能力．
练习册系列答案
轻松夺冠全能掌控卷系列答案
相关题目
如图，在平面直角坐标系xOy中，椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的焦距为2$\sqrt{3}$，且过点（1，$\frac{\sqrt{3}}{2}$），椭圆上顶点为A，过点A作圆（x-1）2+y2=r2（0＜r＜1）的两条切线分别与椭圆E相交于点B，C（不同于点A），设直线AB，AC的斜率分别为kAB，KAC．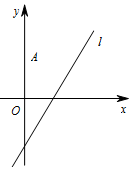
如图，在平面直角坐标系xOy中，点A（0，3），直线l：y=x-1，设圆C的半径为1，圆心在l上．