题目内容
2．
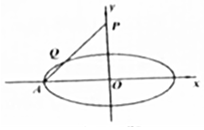如图，过椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的左顶点A作直线交y轴于点P，交椭圆于点Q，若△AOP是等腰三角形，且$\overrightarrow{PQ}$=2$\overrightarrow{QA}$，则椭圆的离心率是$\frac{2\sqrt{5}}{5}$．
分析 利用等腰三角形的性质和向量相等运算即可得出点Q的坐标，再代入椭圆方程即可．
解答 解：∵△AOP是等腰三角形，A（-a，0）∴P（0，a）．
设Q（x0，y0），∵$\overrightarrow{PQ}$=2$\overrightarrow{QA}$，
∴（x0，y0-a）=2（-a-x0，-y0）．
∴$\left\{\begin{array}{l}{{x}_{0}=-2a-2{x}_{0}}\\{{y}_{0}-a=-2{y}_{0}}\end{array}\right.$，解得$\left\{\begin{array}{l}{{x}_{0}=-\frac{2}{3}a}\\{{y}_{0}=\frac{1}{3}a}\end{array}\right.$．
代入椭圆方程得$\frac{\frac{4}{9}{a}^{2}}{{a}^{2}}$+$\frac{\frac{1}{9}{a}^{2}}{{b}^{2}}$=1，化为$\frac{{b}^{2}}{{a}^{2}}$=$\frac{1}{5}$．
∴e=$\frac{c}{a}$=$\sqrt{1-\frac{{b}^{2}}{{a}^{2}}}$=$\frac{2\sqrt{5}}{5}$．
故答案：$\frac{2\sqrt{5}}{5}$
点评 熟练掌握等腰三角形的性质和向量相等运算、“代点法”等是解题的关键．
练习册系列答案
阅读快车系列答案
相关题目
12．复数i（2-i）在复平面内对应的点的坐标为（ ）
| A． | （-2，1） | B． | （2，-1） | C． | （1，2） | D． | （-1，2） |
在四棱锥P-ABCD中，底面ABCD为矩形，AP⊥平面PCD，E，F分别为PC，AB的中点．求证：
如图，在平面直角坐标系xOy中，椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的焦距为2$\sqrt{3}$，且过点（1，$\frac{\sqrt{3}}{2}$），椭圆上顶点为A，过点A作圆（x-1）2+y2=r2（0＜r＜1）的两条切线分别与椭圆E相交于点B，C（不同于点A），设直线AB，AC的斜率分别为kAB，KAC．
14．函数f（x）=x+lg（x-2）的零点所在区间为（ ）
| A． | （2，2.0001） | B． | （2.0001，2.001） | C． | （2.001，2.01） | D． | （2.01，3） |
11．设命题p：?x0∈（0，+∞），lnx0=-1．
命题q：若m＞1，则方程x2+my2=1表示焦点在x轴上的椭圆．
那么，下列命题为真命题的是（ ）
命题q：若m＞1，则方程x2+my2=1表示焦点在x轴上的椭圆．
那么，下列命题为真命题的是（ ）
| A． | ￢q | B． | （￢p）∨（￢q） | C． | p∧q | D． | p∧（￢q） |