题目内容
设函数y=f(x)在(-∞,+∞)内有意义.对于给定的正数k,已知函数fk(x)=
,取函f(x)=3-x-e-x.若对任意的x∈(-∞,+∞),恒有fk(x)=f(x),则k的取值范围为 .
|
考点:函数恒成立问题
专题:计算题,导数的概念及应用
分析:用导数确定函数函数的单调性,求解函数的最值,进而求出k的范围,进一步得出所要的结果.
解答:
解:对任意的x∈(-∞,+∞),恒有fk(x)=f(x),等价于对任意的x∈(-∞,+∞),恒有f(x)=3-x-e-x≤k,
由f'(x)=-1+e-x,知当x∈(-∞,0)时,f'(x)>0,f(x)单调递增;
当x∈(0,+∞)时,f'(x)<0,f(x)单调递减;则f(x)max=f(0)=2;
故k≥2.
故答案为:k≥2.
由f'(x)=-1+e-x,知当x∈(-∞,0)时,f'(x)>0,f(x)单调递增;
当x∈(0,+∞)时,f'(x)<0,f(x)单调递减;则f(x)max=f(0)=2;
故k≥2.
故答案为:k≥2.
点评:本题考查学生对新定义型问题的理解和掌握程度,理解好新定义的分段函数是解决本题的关键,将所求解的问题转化为求解函数的最值问题,利用了导数的工具作用,体现了恒成立问题的解题思想.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目
已知等差数列{an}满足a1+a2+a3+…+a101=0,则a1+a101与0的大小关系为( )
| A、a1+a101>0 |
| B、a1+a101<0 |
| C、a1+a101=0 |
| D、以上皆有可能 |
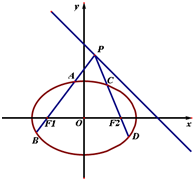 已知椭圆
已知椭圆