题目内容

已知复数z=（2+i）（x-i）为纯虚数，其中i为虚数单位，则实数x的值为
 
．
考点：复数的基本概念
专题：数系的扩充和复数
分析：直接由复数代数形式的乘法运算化简复数z，又复数z为纯虚数，则实部为0，虚部不等于0，即可求出实数x的值．
解答： 解：∵z=（2+i）（x-i）=2x-2i+xi-i2=2x+1+（x-2）i，
又复数z为纯虚数，
∴
2x+1=0
x-2≠0
，
解得：x=-
1
2
．
故答案为：-
1
2
．
点评：本题考查了复数的基本概念，是基础题．
练习册系列答案
相关题目
下列命题中，真命题是（　　）
A、?x0∈R，e x0≤0
B、?x∈R，2x＞x2
C、“a＞1，b＞1”是“ab＞1”的充要条件
D、设
a
，
b
为向量，则“|
a
•
b
|=|
a
||
b
|”是“
a
∥
b
”的充要条件
若直线y=x+b与圆（x-1）2+y2=1有两个不同的公共点，则实数b的取值范围为（　　）
A、（-
2
-1，
2
-1）
B、（-∞，
2
-1）
C、（-∞，-
2
-1）∪（
2
-1，+∞）
D、[-
2
-1，
2
-1]
6个同学任意选3个参加一个会议，共有选法种数（　　）种．
A、15B、10C、60D、20
已知f（x）=
bx+1
2x+a
（其中a，b为常数，且ab≠2），在定义域内任一个x有f(x)•f(
1
x
)=k （k为常数），则k=
 
．
定义在R上的偶函数f（x），当x≥0时，f（x）=x2，则不等式f（1-2x）＜f（3）的解集是
 
．
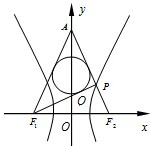如图，已知双曲线
x2
a2
-
y2
b2
=1（a、b＞0）的左右焦点分别为F1、F2，|F1F2|=6，P是双曲线右支上的一点，PF1⊥PF2，F2P与y轴交于点A，△APF1的内切圆半径为
3
，则双曲线的离心率为（　　）
A、2
2
B、
2
C、2
3
D、
3
若函数f（x）=logax（其中a为常数且a＞0，a≠1）满足f（2）＞f（3）且f（
1
2
）=1则f（1-
1
x
）＞1的解集是
 
．
已知等差数列{an}中，a2=7，a4=15，则前20项的和S20=
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网