题目内容
已知数列{an}满足Sn+an=2n+1(nN*),
(1)写出a1,a2,a3,并求an的表达式;
(2)求证:
+
+…+
<
-
•
.
(1)写出a1,a2,a3,并求an的表达式;
(2)求证:
| 2-a1 |
| a1-1 |
| 2-a2 |
| a2-1 |
| 2-an |
| an-1 |
| 5 |
| 3 |
| 7 |
| 6 |
| 1 |
| 2n |
考点:数列与不等式的综合,数列递推式
专题:等差数列与等比数列,不等式的解法及应用
分析:(1)直接由数列递推式求得数列前三项,在数列递推式中,取n=n-1得另一递推式,作差后另一构造法构造等比数列{an-2},然后由等比数列的通项公式得答案;
(2)把(1)中求得的数列的通项公式代入
+
+…+
,化简后另一数学归纳法证明数列不等式
+
+…+
<
-
•
.
(2)把(1)中求得的数列的通项公式代入
| 2-a1 |
| a1-1 |
| 2-a2 |
| a2-1 |
| 2-an |
| an-1 |
| 2-a1 |
| a1-1 |
| 2-a2 |
| a2-1 |
| 2-an |
| an-1 |
| 5 |
| 3 |
| 7 |
| 6 |
| 1 |
| 2n |
解答:
(1)解:由Sn+an=2n+1 ①,得
S1+a1=2a1=3,a1=
.
S2+a2=a1+2a2=5,a2=
.
S3+a3=a1+a2+2a3=7,a3=
.
Sn-1+an-1=2(n-1)+1(n≥2)②,
①-②得an+an-an-1=2,即an=
an-1+1(n≥2).
∴an-2=
(an-1-2)(n≥2).
∴数列{an-2}是以-
为首项,以
为公比的等比数列.
∴an=(-
)×(-
)n-1+2=2-
;
(2)证明:由an=1-
,得
=
.
因此,不等式
+
+…+
<
-
•
等价于
+
+…
<
-
•
.
下面利用数学归纳法证明:
当n=1时,左边=1,右边=
-
=
.
左边<右边,不等式成立;
假设当n=k时不等式成立,即
+
+…+
<
-
•
.
那么,当n=k+1时,
左边=
+
+…+
+
<
-
•
+
=
-
•
+
=
-
•
+
-
•
=
-
•
+
=
-
•
+
.
∵k≥2.
∴7-2k+1<0.
故
<0.
∴
+
+…+
+
<
-
•
.
∴当n=k+1时不等式成立.
综上可知,对于任意的n∈N*,都有
+
+…+
<
-
•
.
S1+a1=2a1=3,a1=
| 3 |
| 2 |
S2+a2=a1+2a2=5,a2=
| 7 |
| 4 |
S3+a3=a1+a2+2a3=7,a3=
| 15 |
| 8 |
Sn-1+an-1=2(n-1)+1(n≥2)②,
①-②得an+an-an-1=2,即an=
| 1 |
| 2 |
∴an-2=
| 1 |
| 2 |
∴数列{an-2}是以-
| 1 |
| 2 |
| 1 |
| 2 |
∴an=(-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2n |
(2)证明:由an=1-
| 1 |
| 2n |
| 2-an |
| an-1 |
| 1 |
| 2n-1 |
因此,不等式
| 2-a1 |
| a1-1 |
| 2-a2 |
| a2-1 |
| 2-an |
| an-1 |
| 5 |
| 3 |
| 7 |
| 6 |
| 1 |
| 2n |
| 1 |
| 2-1 |
| 1 |
| 22-1 |
| 1 |
| 2n-1 |
| 5 |
| 3 |
| 7 |
| 6 |
| 1 |
| 2n |
下面利用数学归纳法证明:
当n=1时,左边=1,右边=
| 5 |
| 3 |
| 7 |
| 12 |
| 13 |
| 12 |
左边<右边,不等式成立;
假设当n=k时不等式成立,即
| 1 |
| 2-1 |
| 1 |
| 22-1 |
| 1 |
| 2k-1 |
| 5 |
| 3 |
| 7 |
| 6 |
| 1 |
| 2k |
那么,当n=k+1时,
左边=
| 1 |
| 2-1 |
| 1 |
| 22-1 |
| 1 |
| 2k-1 |
| 1 |
| 2k+1-1 |
| 5 |
| 3 |
| 7 |
| 6 |
| 1 |
| 2k |
| 1 |
| 2k+1-1 |
=
| 5 |
| 3 |
| 7 |
| 6 |
| 2 |
| 2k+1 |
| 1 |
| 2k+1-1 |
| 5 |
| 3 |
| 7 |
| 6 |
| 1 |
| 2k+1 |
| 1 |
| 2k+1-1 |
| 7 |
| 6 |
| 1 |
| 2k+1 |
=
| 5 |
| 3 |
| 7 |
| 6 |
| 1 |
| 2k+1 |
| 6•2k+1-7(2k+1-1) |
| 6(2k+1-1)•2k+1 |
| 5 |
| 3 |
| 7 |
| 6 |
| 1 |
| 2k+1 |
| 7-2k+1 |
| 6(2k+1-1)•2k+1 |
∵k≥2.
∴7-2k+1<0.
故
| 7-2k+1 |
| 6(2k+1-1)•2k+1 |
∴
| 1 |
| 2-1 |
| 1 |
| 22-1 |
| 1 |
| 2k-1 |
| 1 |
| 2k+1-1 |
| 5 |
| 3 |
| 7 |
| 6 |
| 1 |
| 2k+1 |
∴当n=k+1时不等式成立.
综上可知,对于任意的n∈N*,都有
| 2-a1 |
| a1-1 |
| 2-a2 |
| a2-1 |
| 2-an |
| an-1 |
| 5 |
| 3 |
| 7 |
| 6 |
| 1 |
| 2n |
点评:本题考查了数列递推式,考查了利用构造法求数列的通项公式,训练了利用数学归纳法证明数列不等式,是压轴题.

练习册系列答案
相关题目
设P(x,y)是函数y=
+lnx图象上的点,则x+y的最小值为( )
| 2 |
| x |
| A、3 | ||
| B、2 | ||
C、
| ||
| D、3+ln2 |
使函数y=sin(2x+θ)+
cos(2x+θ)在[-
,0]上是减函数的θ的一个值为( )
| 3 |
| π |
| 4 |
A、
| ||
B、
| ||
C、
| ||
D、
|
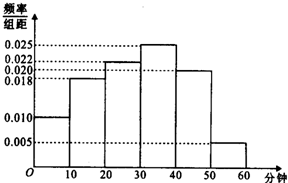 电视传媒公司为了了解某地区电视观众对某类体育节目的收视情况,随机抽取了100名观众进行调查,其中女性有55名.右图是根据调查结果绘制的观众日均收看该体育节目时间的频率分布直方图.将日均收看该体育节目时间不低于40分钟的观众称为“体育迷”,已知“体育迷”中有10名女性.
电视传媒公司为了了解某地区电视观众对某类体育节目的收视情况,随机抽取了100名观众进行调查,其中女性有55名.右图是根据调查结果绘制的观众日均收看该体育节目时间的频率分布直方图.将日均收看该体育节目时间不低于40分钟的观众称为“体育迷”,已知“体育迷”中有10名女性.