题目内容
过双曲线
-
=1(b>a>0)的左顶点A作斜率为1的直线l,l与双曲线的两条渐近线相交于B,C两点,且|AB|=|BC|,则双曲线的离心率为( )
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||
| B、3 | ||
C、
| ||
| D、10 |
考点:双曲线的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:先根据条件求出直线l的方程,联立直线方程与渐近线方程分别求出点B,C的横坐标,结合B为AC的中点求出b,a间的关系,进而求出双曲线的离心率.
解答:
解:由题得:双曲线:的左顶点A(-a,0)
所以所作斜率为1的直线l:y=x+a,
若l与双曲线M的两条渐近线分别相交于点B(x1,y1),C(x2,y2).
联立其中一条渐近线y=-
x,解得x1=
①;
同理联立解得x2=
②;
又因为|AB|=|BC|,
故B是A,C的中点,
∴x1=
⇒2x1=x2-a,
把①②代入整理得:b=3a,
∴e=
=
=
.
故选:C.
所以所作斜率为1的直线l:y=x+a,
若l与双曲线M的两条渐近线分别相交于点B(x1,y1),C(x2,y2).
联立其中一条渐近线y=-
| b |
| a |
| a2 |
| -a-b |
同理联立解得x2=
| a2 |
| b-a |
又因为|AB|=|BC|,
故B是A,C的中点,
∴x1=
| x2-a |
| 2 |
把①②代入整理得:b=3a,
∴e=
| c |
| a |
| 1+32 |
| 10 |
故选:C.
点评:本题考查双曲线性质的综合运用,解题过程中要注意由|AB|=|BC|得到B是A,C的中点这以结论的运用.

练习册系列答案
相关题目
已知集合M={(x,y)|x+y<0,xy>0},N={(x,y)|x<0,y<0},那么( )
| A、N?M | B、M?N |
| C、M=N | D、M?N |
使函数y=sin(2x+θ)+
cos(2x+θ)在[-
,0]上是减函数的θ的一个值为( )
| 3 |
| π |
| 4 |
A、
| ||
B、
| ||
C、
| ||
D、
|
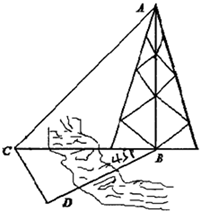 如图,测量河对岸的塔的高度AB,可以选择与B在同一水平面内的两个点C、D.测得由C望A的仰角∠ACB=45°,方位角∠BCD═60°、∠BDC=75°,又测得C、D相距20米.试求塔的高度AB.
如图,测量河对岸的塔的高度AB,可以选择与B在同一水平面内的两个点C、D.测得由C望A的仰角∠ACB=45°,方位角∠BCD═60°、∠BDC=75°,又测得C、D相距20米.试求塔的高度AB.