题目内容
已知函数f(x)=ex-
x2e|x|.
(Ⅰ)若f(x)是[0,+∞)上是增函数,求实数a的取值范围;
(Ⅱ)证明:当a≥1时,证明不等式f(x)≤x+1对x∈R恒成立;
(Ⅲ)对于在(0,1)中的任一个常数a,试探究是否存在x0>0,使得f(x0)>x0+1成立?如果存在,请求出符合条件的一个x0;如果不存在,请说明理由.
| a |
| 2 |
(Ⅰ)若f(x)是[0,+∞)上是增函数,求实数a的取值范围;
(Ⅱ)证明:当a≥1时,证明不等式f(x)≤x+1对x∈R恒成立;
(Ⅲ)对于在(0,1)中的任一个常数a,试探究是否存在x0>0,使得f(x0)>x0+1成立?如果存在,请求出符合条件的一个x0;如果不存在,请说明理由.
考点:导数在最大值、最小值问题中的应用
专题:导数的综合应用
分析:(Ⅰ)当x≥0时,f(x)=ex(1-
x2),通过求导研究函数的性质,即f'(x)≥0在[0,+∞)上恒成立.
(Ⅱ)分成x≥0和x<0两种情况分别谈论.当x≥0时,原不等式可化为
x2+
≥1,下面只需要通过求导的方法研究函数
x2+
的最小值即可;当x<0时,原不等式可化为
x2e-2x+(x+1)e-x≥1,同理,通过求导的方法研究函数
x2e-2x+(x+1)e-x的最小值即可,同时注意题目中条件“a≥1”运用.
(Ⅲ)假设存在这样的x0>0满足条件,即需
+
-1<0,也就是对于函数t(x)=
+
-1,满足t(x)min<0即可.然后依旧用求导的方式进行研究,注意到基于其最小值t(x0)=
(lna)2+a(-lna+1)-1的复杂性,仍需要用求导的方式证明
(lna)2-alna+a-1<0.
| a |
| 2 |
(Ⅱ)分成x≥0和x<0两种情况分别谈论.当x≥0时,原不等式可化为
| a |
| 2 |
| x+1 |
| ex |
| a |
| 2 |
| x+1 |
| ex |
| a |
| 2 |
| a |
| 2 |
(Ⅲ)假设存在这样的x0>0满足条件,即需
a
| ||
| 2 |
| x0+1 |
| ex0 |
a
| ||
| 2 |
| x+1 |
| ex |
| a |
| 2 |
| a |
| 2 |
解答:
解:(I)∵x∈[0,+∞)时,f(x)=ex(1-
x2),
∴f′(x)=ex(-
x2-ax+1).
由题意,f'(x)≥0在[0,+∞)上恒成立,
当a=0时,f'(x)=ex>0恒成立,即满足条件.
当a≠0时,要使f'(x)≥0,而ex>0恒成立,
故只需-
x2-ax+1≥0在[0,+∞)上恒成立,结合着-
x2-ax+1的对称轴方程是x=-1,
∴
解得a<0.
综上,a的取值范围为a≤0.
(Ⅱ)由题知f(x)≤x+1即为ex-
x2e|x|≤x+1.
①在x≥0时,要证明ex-
x2e|x|≤x+1成立,
只需证ex≤
x2ex+x+1,即证1≤
x2+
,①
令g(x)=
x2+
,得g′(x)=ax+
=ax-
,
整理得g′(x)=x(a-
),
∵x≥0时,
≤1,结合a≥1,得g'(x)≥0,
∴g(x)为在[0,+∞)上是增函数,故g(x)≥g(0)=1,从而①式得证.
②在x≤0时,要使ex-
x2e|x|≤x+1成立,
只需证ex≤
x2e-x+x+1,即证1≤
x2e-2x+(x+1)e-x,②
令m(x)=
e-2x+(x+1)e-x,得m'(x)=-xe-2x[ex+a(x-1)],
而φ(x)=ex+a(x-1)在x≤0时为增函数,
故φ(x)≤φ(0)=1-a≤0,从而m'(x)≤0,
∴m(x)在x≤0时为减函数,则m(x)≥m(0)=1,从而②式得证.
综上所述,原不等式ex-
x2e|x|≤x+1即f(x)≤x+1在a≥1时恒成立.
(Ⅲ)要使f(x0)>x0+1成立,即ex0-
x02ex0>x0+1,
变形为
+
-1<0,③
要找一个x0>0使③式成立,只需找到函数t(x)=
+
-1的最小值,满足t(x)min<0即可.
∵t′(x)=x(a-
),
令t'(x)=0得ex=
,则x=-lna,取x0=-lna,
在0<x<-lna时,t'(x)<0,在x>-lna时,t'(x)>0,
即t(x)在(0,-lna)上是减函数,在(-lna,+∞)上是增函数,
∴当x=-lna时,t(x)取得最小值t(x0)=
(lna)2+a(-lna+1)-1
下面只需证明:
(lna)2-alna+a-1<0在0<a<1时成立即可.
又令p(a)=
(lna)2-alna+a-1,
则p′(a)=
(lna)2≥0,从而p(a)在(0,1)上是增函数,
则p(a)<p(1)=0,从而
(lna)2-alna+a-1<0,得证.
于是t(x)的最小值t(-lna)<0,
因此可找到一个常数x0=-lna(0<a<1),使得③式成立.
| a |
| 2 |
∴f′(x)=ex(-
| a |
| 2 |
由题意,f'(x)≥0在[0,+∞)上恒成立,
当a=0时,f'(x)=ex>0恒成立,即满足条件.
当a≠0时,要使f'(x)≥0,而ex>0恒成立,
故只需-
| a |
| 2 |
| a |
| 2 |
∴
|
综上,a的取值范围为a≤0.
(Ⅱ)由题知f(x)≤x+1即为ex-
| a |
| 2 |
①在x≥0时,要证明ex-
| a |
| 2 |
只需证ex≤
| a |
| 2 |
| a |
| 2 |
| x+1 |
| ex |
令g(x)=
| a |
| 2 |
| x+1 |
| ex |
| 1•ex-(x+1)ex |
| (ex)2 |
| x |
| ex |
整理得g′(x)=x(a-
| 1 |
| ex |
∵x≥0时,
| 1 |
| ex |
∴g(x)为在[0,+∞)上是增函数,故g(x)≥g(0)=1,从而①式得证.
②在x≤0时,要使ex-
| a |
| 2 |
只需证ex≤
| a |
| 2 |
| a |
| 2 |
令m(x)=
| ax2 |
| 2 |
而φ(x)=ex+a(x-1)在x≤0时为增函数,
故φ(x)≤φ(0)=1-a≤0,从而m'(x)≤0,
∴m(x)在x≤0时为减函数,则m(x)≥m(0)=1,从而②式得证.
综上所述,原不等式ex-
| a |
| 2 |
(Ⅲ)要使f(x0)>x0+1成立,即ex0-
| a |
| 2 |
变形为
a
| ||
| 2 |
| x0+1 |
| ex0 |
要找一个x0>0使③式成立,只需找到函数t(x)=
a
| ||
| 2 |
| x+1 |
| ex |
∵t′(x)=x(a-
| 1 |
| ex |
令t'(x)=0得ex=
| 1 |
| a |
在0<x<-lna时,t'(x)<0,在x>-lna时,t'(x)>0,
即t(x)在(0,-lna)上是减函数,在(-lna,+∞)上是增函数,
∴当x=-lna时,t(x)取得最小值t(x0)=
| a |
| 2 |
下面只需证明:
| a |
| 2 |
又令p(a)=
| a |
| 2 |
则p′(a)=
| 1 |
| 2 |
则p(a)<p(1)=0,从而
| a |
| 2 |
于是t(x)的最小值t(-lna)<0,
因此可找到一个常数x0=-lna(0<a<1),使得③式成立.
点评:本题在导数的综合应用中属于难题,特别是在(2)(3)两小问的解答中,比较繁琐,如(2)中,既要用到分类讨论的思想,又要变换形式,分别求导.这也是提醒考生,解题时遇到含绝对值的式子时,往往还是需要分类讨论使得式子可解;(3)中,“存在”思想的运用是考生容易混淆的知识点之一,即存在x0>0,使得f(x0)>x0+1成立,只需要[f(x)-x-1]max>0即可,这个思想的运用对于学生来说,相对比较难,也要和恒成立问题中的思想区别开来.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案
相关题目
一个算法的程序框图如图所示,如果输入的x的值为2014,则输出的i的结果为( )
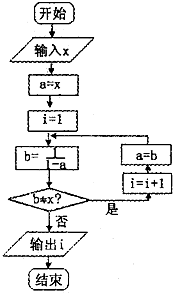

| A、3 | B、5 | C、6 | D、8 |