题目内容
若椭圆x2+my2=1的离心率e∈(
,
),则m的取值范围是( )
| ||
| 3 |
| ||
| 2 |
| A、(1,2) | ||||||
B、(
| ||||||
C、(
| ||||||
D、(
|
考点:椭圆的简单性质
专题:圆锥曲线的定义、性质与方程
分析:首先,分两种情形,焦点在x轴上和焦点在y轴上,然后,借助于离心率e∈(
,
),确定m的取值范围.
| ||
| 3 |
| ||
| 2 |
解答:
解:∵椭圆x2+my2=1,
∴
+
=1,
当椭圆的焦点在x轴上时,
即0<
<1时,解得m>1,
∵a=1,c=
,
∴e=
=
∈(
,
),
∴
<m<2,
当焦点在y轴上时,即
>1,
即0<m<1,
∵a=
,c=
,
∴e=
=
∈(
,
),
∴
<m<
,
综上,实数m的取值范围为(
,
)∪(
,2).
故选:C.
∴
| x2 |
| 1 |
| y2 | ||
|
当椭圆的焦点在x轴上时,
即0<
| 1 |
| m |
∵a=1,c=
1-
|
∴e=
| c |
| a |
1-
|
| ||
| 3 |
| ||
| 2 |
∴
| 3 |
| 2 |
当焦点在y轴上时,即
| 1 |
| m |
即0<m<1,
∵a=
|
|
∴e=
| c |
| a |
| ||||
|
| ||
| 3 |
| ||
| 2 |
∴
| 1 |
| 2 |
| 2 |
| 3 |
综上,实数m的取值范围为(
| 1 |
| 2 |
| 2 |
| 3 |
| 3 |
| 2 |
故选:C.
点评:本题重点考查了椭圆的方程、椭圆的简单几何性质等知识,属于中档题,切实掌握分类讨论思想在求解解析几何问题中的运用.

练习册系列答案
 每课必练系列答案
每课必练系列答案 巧学巧练系列答案
巧学巧练系列答案
相关题目
设z=a+bi(a,b∈R),则z为纯虚数的必要不充分条件是( )
| A、a≠0且b=0 |
| B、a≠0且b≠0 |
| C、a=0 |
| D、a=0且b≠0 |
已知函数y=f(x)的定义域是数集A,若对于任意a,b∈A,当a<b时,都有f(a)<f(b),则方程f(x)的实数根为( )
| A、有且只有一个 |
| B、一个都没有 |
| C、至多有一个 |
| D、可能会有两个或两个以上 |
平面α截一个三棱锥,如果截面是梯形,那么平面α必定和这个三棱锥的( )
| A、一个侧面平行 |
| B、底面平行 |
| C、仅一条侧棱平行 |
| D、某两条相对的棱都平行 |
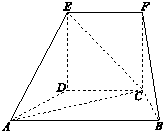 如图所示的几何体中,面CDEF为正方形,面ABCD为等腰梯形,AB∥CD,AB=2BC,∠ABC=60°,且平面CDEF⊥平面ABCD.
如图所示的几何体中,面CDEF为正方形,面ABCD为等腰梯形,AB∥CD,AB=2BC,∠ABC=60°,且平面CDEF⊥平面ABCD.