Question

一船向正北航行，看见正西方有两个灯塔恰好与它在一条直线上，两塔相距10海里，继续航行半小时后看见一塔在船的南偏西60°，另一塔在船的南偏西45°，则船速是

 

海里/小时．

Answer 1

考点：解三角形的实际应用

专题：应用题,解三角形

分析：由题意作出示意图，先在△ABC中，由正弦定理求得CB，再在Rt△CBD中通过解直角三角形求出CO，则船速v=

CO

0.5

．

解答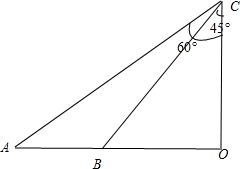： 解：如图所示：
船初始位置为O点，半小时后到C点，
由题意知∠CBO=45°，∠CAB=30°，AB=10，∠ACB=15°，
在△ABC中，由正弦定理得，

AB

sin15°

=

CB

sin30°

，
解得CB=5（

6

+

2

），
在Rt△CBD中，CO=BC•sin45°=5（

6

+

2

）•

2

2

=5（

3

+1），
则船速v=

CO

0.5

=5（

3

+1）×2=10(

3

+1)．
故答案为：10(

3

+1)．

点评：本题考查正弦定理，考查学生利用所学数学知识分析解决实际问题的能力，考查学生的运算能力，属中档题．