题目内容
已知函数f(x)=lnx-a(x-1),g(x)=ex.
(Ⅰ)求函数f(x)的单调区间;
(Ⅱ)过原点分别作函数f(x)与g(x)的切线,且两切线的斜率互为倒数,证明:a=0或1<a<2;
(Ⅲ)求证:(1+
)(1+
)(1+
)…[1+
]<e(其中n∈N*,ex是自然对数的底).
(Ⅰ)求函数f(x)的单调区间;
(Ⅱ)过原点分别作函数f(x)与g(x)的切线,且两切线的斜率互为倒数,证明:a=0或1<a<2;
(Ⅲ)求证:(1+
| 2 |
| 2×3 |
| 4 |
| 3×5 |
| 8 |
| 5×9 |
| 2n |
| (2n-1+1)(2n+1) |
考点:利用导数研究函数的单调性,利用导数研究曲线上某点切线方程,数列的求和
专题:计算题,证明题,导数的综合应用
分析:(Ⅰ)求函数的导数即可求函数f(x)的单调区间;
(Ⅱ)根据导数的几何意义,求出切线的斜率,建立条件关系即可得到结论;
(Ⅲ)利用ln(x+1)≤x在[0,+∞)上恒成立,利用此不等式对所要证明的不等式进行放缩,从而进行证明.
(Ⅱ)根据导数的几何意义,求出切线的斜率,建立条件关系即可得到结论;
(Ⅲ)利用ln(x+1)≤x在[0,+∞)上恒成立,利用此不等式对所要证明的不等式进行放缩,从而进行证明.
解答:
(1)解:f′(x)=
-a(x>0),
①当a≤0时,f'(x)>0,增区间是(0,+∞);
②当a>0时,增区间是(0,
),减区间是(
,+∞);
(2)证明:设g(x)的切点(x1,y1),f(x)的切点(x2,y2),
解得
,
∴
,
∴
-a=
,
∴lnx2=1-a,∴x2=e1-a,代入
-a=
,得ea-ae-1=0,
令p(a)=ea-ae-1,p'(a)=ea-e,
p(a)在(-∞,1)递减,在(1,+∞)上递增,
当a∈(-∞,1)时,
∵p(0)=0,∴a=0;
当a∈(1,+∞)时,p(1)=-1<0,p(2)=e2-2e-1>0,所以1<a<2,
综上a=0或1<a<2.
(Ⅲ)证明:令h(x)=ln(1+x)-x(x>0),则h′(x)=
-1<0,
则h(x)在x>0时为减函数,则h(x)<h(0)=0,即有ln(1+x)<x,
又
=2(
-
)
则ln{(1+
)(1+
)(1+
)…[1+
]}
=ln(1+
)+ln(1+
)+ln(1+
)+…+ln[1+
]
<
+
+…+
=2(
-
+
-
+…+
-
)
=2(
-
)<1,
则有(1+
)(1+
)(1+
)…[1+
]<e.
| 1 |
| x |
①当a≤0时,f'(x)>0,增区间是(0,+∞);
②当a>0时,增区间是(0,
| 1 |
| a |
| 1 |
| a |
(2)证明:设g(x)的切点(x1,y1),f(x)的切点(x2,y2),
|
|
∴
|
∴
| 1 |
| x2 |
| lnx2-a(x2-1) |
| x2 |
∴lnx2=1-a,∴x2=e1-a,代入
| 1 |
| x2 |
| 1 |
| e |
令p(a)=ea-ae-1,p'(a)=ea-e,
p(a)在(-∞,1)递减,在(1,+∞)上递增,
当a∈(-∞,1)时,
∵p(0)=0,∴a=0;
当a∈(1,+∞)时,p(1)=-1<0,p(2)=e2-2e-1>0,所以1<a<2,
综上a=0或1<a<2.
(Ⅲ)证明:令h(x)=ln(1+x)-x(x>0),则h′(x)=
| 1 |
| x+1 |
则h(x)在x>0时为减函数,则h(x)<h(0)=0,即有ln(1+x)<x,
又
| 2n |
| (2n-1+1)(2n+1) |
| 1 |
| 2n-1+1 |
| 1 |
| 2n+1 |
则ln{(1+
| 2 |
| 2×3 |
| 4 |
| 3×5 |
| 8 |
| 5×9 |
| 2n |
| (2n-1+1)(2n+1) |
=ln(1+
| 2 |
| 2×3 |
| 4 |
| 3×5 |
| 8 |
| 5×9 |
| 2n |
| (2n-1+1)(2n+1) |
<
| 2 |
| 2×3 |
| 4 |
| 3×5 |
| 2n |
| (2n-1+1)(2n+1) |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 2n-1+1 |
| 1 |
| 2n+1 |
=2(
| 1 |
| 2 |
| 1 |
| 2n+1 |
则有(1+
| 2 |
| 2×3 |
| 4 |
| 3×5 |
| 8 |
| 5×9 |
| 2n |
| (2n-1+1)(2n+1) |
点评:本题主要考查函数的单调区间的求解,以及导数的几何意义,考查导数的基本运算,考查不等式的证明要借助所给函数构造不等式,利用它进行放缩证明,本题难度比较大,是一道综合题.

练习册系列答案
相关题目
若{an}是等比数列,若a1=1,S6=4S3,则a4=( )
| A、0 | B、1 | C、2 | D、3 |
已知函数f(x)=3x3-2x,则f(2)+f(-2)=( )
| A、-2 | B、-40 | C、44 | D、0 |
直线x-y+2=0的倾斜角为( )
| A、60° | B、120° |
| C、45° | D、135° |
阅读如图所示的程序框图,若输入的x=4,则运行该程序后输出的实数y等于( )


| A、1 | B、2 | C、4 | D、9 |
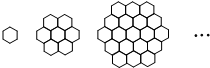 蜜蜂被认为是自然界中最杰出的建筑师,单个蜂巢可以近似地看作是一个正六边形,如图为一组蜂巢的截面图.其中第一个图有1个蜂巢,第二个图有7个蜂巢,第三个图有19个蜂巢,按此规律,以f(n)表示第n幅图的蜂巢总数.则f(10)=
蜜蜂被认为是自然界中最杰出的建筑师,单个蜂巢可以近似地看作是一个正六边形,如图为一组蜂巢的截面图.其中第一个图有1个蜂巢,第二个图有7个蜂巢,第三个图有19个蜂巢,按此规律,以f(n)表示第n幅图的蜂巢总数.则f(10)=