题目内容
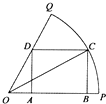 如图,已知OPQ是半径为
如图,已知OPQ是半径为| 7 |
| π |
| 3 |
(1)当α=
| π |
| 6 |
(2)求
| OA |
| OB |
考点:平面向量数量积的运算,弧度制的应用
专题:平面向量及应用
分析:(Ⅰ)在Rt△OBC中,由条件利用直角三角形中的边角关系求得BC、OB的值,可得OA=AD•tan
=
BC的值.
(Ⅱ)由条件利用三角恒等变换化简
•
为
sin(2α+
)-
,再根据 0<α<
,利用正弦函数的定义域和值域求得它的最大值.
| π |
| 6 |
| ||
| 3 |
(Ⅱ)由条件利用三角恒等变换化简
| OA |
| AB |
| 7 |
| 3 |
| π |
| 6 |
| 7 |
| 6 |
| π |
| 3 |
解答:
解:(Ⅰ)在Rt△OBC中,BC=
sin
=
,OB=
cos
=
.
在Rt△ODA中,∠AOD=
∠ODA=
,∴OA=AD•tan
=
BC=
,
AB=OB-OA=
-
=
.
(Ⅱ)在Rt△OBC中,BC=
sinα,OB=
cosα.
在Rt△ODA中,∴OA=DA•tan
=
BC=
sinα,
∴AB=OB-OA=
(cosα-
sinα),则
•
=OA•AB=
(cosα-
sinα)•
sinα
=
(cosα-
sinα)•sinα=
(sinαcosα-
sin2α )
=
•[
sin2α-
(1-cos2α)]=
•[
(
sin2α+
cos2α)-
]
=
sin(2α+
)-
.
∵0<α<
,∴
<2α+
<
,故当2α+
=
时,即α=
时,
•
取得最大值为
.
| 7 |
| π |
| 6 |
| ||
| 2 |
| 7 |
| π |
| 6 |
| ||
| 2 |
在Rt△ODA中,∠AOD=
| π |
| 3 |
| π |
| 6 |
| π |
| 6 |
| ||
| 3 |
| ||
| 6 |
AB=OB-OA=
| ||
| 2 |
| ||
| 6 |
| ||
| 3 |
(Ⅱ)在Rt△OBC中,BC=
| 7 |
| 7 |
在Rt△ODA中,∴OA=DA•tan
| π |
| 6 |
| ||
| 3 |
| ||
| 3 |
∴AB=OB-OA=
| 7 |
| ||
| 3 |
| OA |
| AB |
| 7 |
| ||
| 3 |
| ||
| 3 |
=
7
| ||
| 3 |
| ||
| 3 |
7
| ||
| 3 |
| ||
| 3 |
=
7
| ||
| 3 |
| 1 |
| 2 |
| ||
| 6 |
7
| ||
| 3 |
| 1 | ||
|
| ||
| 2 |
| 1 |
| 2 |
| ||
| 6 |
=
| 7 |
| 3 |
| π |
| 6 |
| 7 |
| 6 |
∵0<α<
| π |
| 3 |
| π |
| 6 |
| π |
| 6 |
| 5π |
| 6 |
| π |
| 6 |
| π |
| 2 |
| π |
| 6 |
| OA |
| AB |
| 7 |
| 6 |
点评:本题主要考查两个向量的数量积的定义,三角恒等变换,正弦函数的定义域和值域,属于基础题.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目
已知⊙C:x2+y2=9中弦AB的长为3
,则
•
=( )
| 2 |
| AB |
| AC |
| A、0 | ||
| B、3 | ||
| C、9 | ||
D、9
|
若复数z满足
=2+i(其中i为虚数单位),则z的共轭复数为( )
| z+i |
| i |
| A、-1-i | B、1-i |
| C、-1+i | D、1+i |
在长为10厘米的线段AB上任取一点G,以AG为半径作圆,则圆的面积介于36π平方厘米到64π平方厘米的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
x2<1是-1<x<1的什么条件( )
| A、充分必要条件 |
| B、必要不充分条件 |
| C、充分不必要条件 |
| D、既不充分与不必要 |