题目内容
已知2 x2+x≤(
)x-2,求函数y=2x+2-x的值域.
| 1 |
| 4 |
考点:指、对数不等式的解法,函数的值域
专题:函数的性质及应用
分析:利用已知不等式得到x的范围,然后求函数的值域.
解答:
解:由2 x2+x≤(
)x-2,得2 x2+x≤24-2x,所以x2+x≤4-2x,解得-4≤x≤1,
所以
≤2x≤2,设2x=t,则y=t+
≥2,当且仅当t=1时等号成立,当t=16,ymax=16+
=16
;
所以函数y=2x+2-x的值域为[2,16
]
| 1 |
| 4 |
所以
| 1 |
| 16 |
| 1 |
| t |
| 1 |
| 16 |
| 1 |
| 16 |
所以函数y=2x+2-x的值域为[2,16
| 1 |
| 16 |
点评:本题考查了指数不等式的加法以及换元法求函数的值域,属于中档题.

练习册系列答案
相关题目
下列函数中,在区间(0,2)上为增函数的是( )
| A、y=2-x | ||
B、y=
| ||
C、y=-log
| ||
| D、y=-x2+2x+3 |
已知全集U=R,集合A={1,2,3,4,5},B={x∈R|
≤0},则A∩B=( )
| x+2 |
| x-3 |
| A、{1,2} |
| B、{x|-2≤x<3} |
| C、{x|0≤x<3} |
| D、{0,1} |
已知正方形OABC的四个顶点分别是0(0,0),A(1,0),B(1,1),C(0,1)设u=x2-y2,v=2xy是一个由平面xOy到平面uOv上的变换,则正方形OABC在这个变换下的图形是( )
A、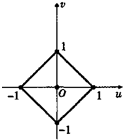 |
B、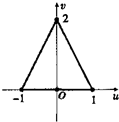 |
C、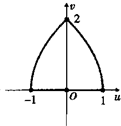 |
D、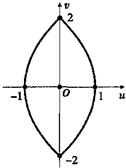 |
设{an}是等差数列,若a5=log
8,则a4+a6等于( )
2 |
| A、6 | B、8 | C、9 | D、16 |
已知
=(1,2),
=(-2,-4),则
与
( )
| a |
| b |
| a |
| b |
| A、平行且反向 |
| B、平行且同向 |
| C、垂直 |
| D、既不平行也不垂直 |