题目内容

已知正方形OABC的四个顶点分别是0（0，0），A（1，0），B（1，1），C（0，1）设u=x2-y2，v=2xy是一个由平面xOy到平面uOv上的变换，则正方形OABC在这个变换下的图形是（　　）
A、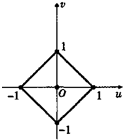
B、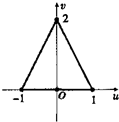
C、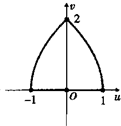
D、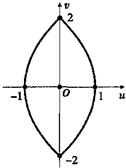
考点：函数的图象与图象变化
专题：计算题,函数的性质及应用
分析：由题意，分x与y同号，异号讨论，从而求解．
解答： 解：正方形满足：|x|+|y|=1，
则若x与y同号，
则u=x2-y2=（|x|+|y|）（|x|-|y|）=|x|-|y|，
v=2|x||y|，
则u2=（|x|+|y|）2-4|x||y|=1-2v，
故v=
1-u2
2
，（-1≤u≤1），
同理，当x与y异号时，
v=
u2-1
2
，（-1≤u≤1），
故选D．
点评：本题考查了函数图象的变换，属于基础题．
练习册系列答案
相关题目
某知名保健品企业新研发了一种健康饮品，已知每天生产该种饮品最多不超过40千瓶，最少1千瓶，经检测在生产过程中该饮品的正品率P与每日生产产品瓶数x（x∈N*，单位：千瓶）间的关系为P=
4200-x2
4500
，每生产一瓶饮品盈利4元，每出现一瓶次品亏损2元（注：正品率=饮品的正品瓶数÷饮品总瓶数×100%）
（Ⅰ）将日利润y（元）表示成日产量x的函数；
（Ⅱ）求该种饮品日利润的最大值．
若x0是函数f（x）=（
1
2
）x-x
1
3
的零点，则x0属于区间
 
．
偶函数f（x）满足f（x-1）=f（x+1），且在x∈[0，1]时，f（x）=-x+1，则关于x的方程f（x）=（
1
10
）x，在x∈[1，3]上解的个数是（　　）
A、1B、2C、3D、4
若直线mx+y-2m=0与直线（3m-4）x+y+1=0垂直的一个充分不必要条件是（　　）
A、m=2
B、m=1或m=
1
3
C、m=1
D、m=-
1
3
已知2 x2+x≤（
1
4
）x-2，求函数y=2x+2-x的值域．
已知f（x）是奇函数，g（x）是偶函数，且f（-1）+g（1）=2，f（1）+g（-1）=4，则g（1）=（　　）
A、4B、3C、2D、1
已知等差数列{an}的首项a1=16，公差d=-
3
4
，当|an|最小时的n值为
 
．
若
cos(π+α)•sin2(-α)
sin(π+α)•cos2(-α)
=
1
2
，则tanα的值为
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网