题目内容

设{an}是等差数列，若a5=log
 
 
2
8，则a4+a6等于（　　）
A、6B、8C、9D、16
考点：等差数列的性质
专题：计算题,等差数列与等比数列
分析：根据a4+a6=2a5，即可得出结论．
解答： 解：由题意，a5=log
 
 
2
8=3，
∵{an}是等差数列，
∴a4+a6=2a5=6，
故选：A．
点评：本题主要考查了等差数列中的等差中项的性质，比较基础．
练习册系列答案
相关题目
设抛物线的顶点在原点，准线方程为x=-1，则抛物线的方程为
 
．
已知2 x2+x≤（
1
4
）x-2，求函数y=2x+2-x的值域．
已知
a
=（3，2），
b
=（-1，2），
c
=（4，1），当k为何值时，（
a
+k
c
）∥（2
b
-
a
）平行时它们是同向还是反向？
已知等差数列{an}的首项a1=16，公差d=-
3
4
，当|an|最小时的n值为
 
．
（Ⅰ）已知2x+2-x=5，求4x+4-x的值；
（Ⅱ）化简2(
32
×
3
)6+(
2
2
)
4
3
-4(
16
49
)-
1
2
-
42
×80.25+(-2005)0．
若集合A={x|log2x＜0}，集合B={x|（
1
2
）x≤1}，则A∩B=（　　）
A、{x|0＜x＜1}
B、{x|0≤x＜1}
C、∅
D、{x|x＞1}
函数y=
2sinx-1
+lg（1-x2）的定义域是
 
．
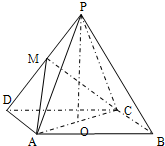如图，在四棱锥P-ABCD中，底面ABCD为平行四边形，∠ADC=45°，AD=AC，O为AC中点，PO⊥平面ABCD，M为PD中点．若AC=2PO，求二面角P-AB-C的正切值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网