题目内容
| ∫ | 0 -
|
考点:微积分基本定理
专题:导数的综合应用
分析:根据微积分的基本定理即可得到结论.
解答:
解:
(sin2x)dx=
(sin2x)d(2x)=
×(-cos2x)|
=
×(-1-1)=-1,
故答案为:-1
| ∫ | 0 -
|
| 1 |
| 2 |
| ∫ | 0 -
|
| 1 |
| 2 |
0 -
|
| 1 |
| 2 |
故答案为:-1
点评:本题主要考查微积分定理的应用,要求熟练掌握常见函数的积分.

练习册系列答案
相关题目
已知双曲线
-
=1(a,b>0)抛物线y2=4x共焦点,双曲线与抛物线的一公共点到抛物线准线的距离为2,双曲线的离心率为e,则2e-b2的值是( )
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||
B、2
| ||
C、4-2
| ||
| D、4 |
 如图,如果你在海边沿着海岸线直线前行,请设计一种测量海中两个小岛A,B之间距离的方法.
如图,如果你在海边沿着海岸线直线前行,请设计一种测量海中两个小岛A,B之间距离的方法.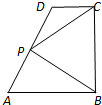 如图,在直角梯形ABCD中,AB∥CD,AB⊥BC,AB=2,CD=1,BC=a(a>0),P为线段AD(含端点)上一个动点,设
如图,在直角梯形ABCD中,AB∥CD,AB⊥BC,AB=2,CD=1,BC=a(a>0),P为线段AD(含端点)上一个动点,设