题目内容
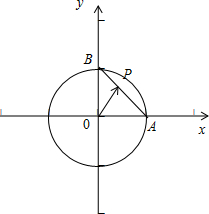
已知A,B是圆O:x2+y2=1上的两个动点,P是AB线段上的动点,当△AOB的面积最大时,则
2-
•
的最小值是( )
| AP |
| AO |
| AP |
A、-
| ||||
| B、0 | ||||
C、-
| ||||
D、-
|
考点:平面向量数量积的运算
专题:计算题,平面向量及应用,直线与圆
分析:由题意知当∠AOB=
时,S取最大值
,此时
⊥
,建立坐标系可得A、B、P的坐标,可得
2-
•
为关于x的二次函数,由二次函数的最值可得.
| π |
| 2 |
| 1 |
| 2 |
| OA |
| OB |
| AP |
| AO |
| AP |
解答:
 解:由题意知:△AOB的面积S=
解:由题意知:△AOB的面积S=
|
||
|sin∠AOB
=
×1×1×sin∠AOB=
sin∠AOB,
当∠AOB=
时,S取最大值
,此时
⊥
,
如图所示,不妨取A(1,0),B(0,1),设P(x,1-x),
∴
2-
•
=
•(
-
)=
•
=(x-1,1-x)•(x,1-x)
=x(x-1)+(1-x)(1-x)
=2x2-3x+1,x∈[0,1]
当x=-
=
时,上式取最小值-
.
故选A.
 解:由题意知:△AOB的面积S=
解:由题意知:△AOB的面积S=| 1 |
| 2 |
| OA |
| OB |
=
| 1 |
| 2 |
| 1 |
| 2 |
当∠AOB=
| π |
| 2 |
| 1 |
| 2 |
| OA |
| OB |
如图所示,不妨取A(1,0),B(0,1),设P(x,1-x),
∴
| AP |
| AO |
| AP |
| AP |
| AP |
| AO |
| AP |
| OP |
=(x-1,1-x)•(x,1-x)
=x(x-1)+(1-x)(1-x)
=2x2-3x+1,x∈[0,1]
当x=-
| -3 |
| 2×2 |
| 3 |
| 4 |
| 1 |
| 8 |
故选A.
点评:本题考查平面向量的数量积的运算,涉及三角形的面积公式和二次函数的最值,属中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
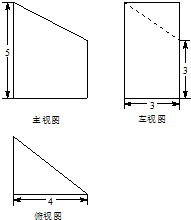
某几何体的三视图如图所示,则该几何体的体积为( )

| A、26 | ||
B、42+3
| ||
| C、62 | ||
D、42-3
|
把函数y=tanx(x∈{x|x≠
+kπ,k∈Z}的图象上所有点向左平行移动
个单位长度,再把所得图象上所有点的横坐标缩短到原来的
倍(纵坐标不变),得到的图象所表示的函数解析式是( )
| π |
| 2 |
| π |
| 3 |
| 1 |
| 2 |
A、y=tan(2x-
| ||||
B、y=tan(
| ||||
C、y=tan(2x+
| ||||
D、y=tan(2x+
|