题目内容
已知两点F1（-1，0）、F2（1，0），且|F1F2|是|PF1|与|PF2|的等差中项，求动点P的轨迹方程．
考点：椭圆的定义
专题：圆锥曲线的定义、性质与方程
分析：由题意以及椭圆的定义得出点P的轨迹是以F1、F2为焦点，长轴是4的椭圆，求出a、b，写出椭圆的方程．
解答：
解：∵F1（-1，0）、F2（1，0），
∴|F1F2|=2；
又∵|F1F2|是|PF1|与|PF2|的等差中项，
∴|PF1|+|PF2|=2|F1F2|=4；
∴点P的轨迹是以F1、F2为焦点，长轴是4的椭圆，
∴a=2，c=1，b=
，
∴椭圆的方程是
+
=1．
∴|F1F2|=2；
又∵|F1F2|是|PF1|与|PF2|的等差中项，
∴|PF1|+|PF2|=2|F1F2|=4；
∴点P的轨迹是以F1、F2为焦点，长轴是4的椭圆，
∴a=2，c=1，b=
| 3 |
∴椭圆的方程是
| x2 |
| 4 |
| y2 |
| 3 |
点评：本题考查了利用椭圆的定义求点的轨迹的问题，解题时应根据椭圆的定义，可以直接写出轨迹方程，是基础题．
练习册系列答案
相关题目
已知圆E的圆心在x轴上，且与y轴切于原点．过抛物线y2=2px（p＞0）焦点F作垂直于x轴的直线l分别交圆和抛物线于A、B两点．已知l截圆所得的弦长为
如图，设点P在曲线y=x2，从原点向A（2，4）移动，让直线OP与曲线y=x2所围成图形面积为S1，直线OP、直线x=2与曲线y=x2所围成图形的面积为S2．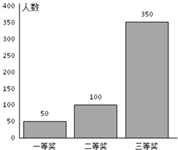
某超市进行促销活动，规定消费者消费每满100元可抽奖一次．抽奖规则：从装有三种只有颜色不同的球的袋中随机摸出一球，记下颜色后放回，依颜色分为一、二、三等奖，一等奖奖金15元，二等奖奖金10元，三等奖奖金5元．活动以来，中奖结果统计如图所示．消费者甲购买了238元的商品，准备参加抽奖．以频率作为概率，解答下列各题．