题目内容
设等差数列{an}的公差为d,Sn是{an}中从第2n-1项开始的连续2n-1项的和,即:
S1=a1,
S2=a2+a3,
S3=a4+a5+a6+a7,
…
Sn=a 2n-1+a 2n-1+1+…+a 2n-1,
…
(1)当a1=3,d=2时,求S4
(2)若S1,S2,S3成等比数列,问:数列{Sn}是否成等比数列?请说明你的理由.
S1=a1,
S2=a2+a3,
S3=a4+a5+a6+a7,
…
Sn=a 2n-1+a 2n-1+1+…+a 2n-1,
…
(1)当a1=3,d=2时,求S4
(2)若S1,S2,S3成等比数列,问:数列{Sn}是否成等比数列?请说明你的理由.
考点:等比数列的性质,数列的求和
专题:综合题,等差数列与等比数列
分析:(1)求出an=2n+1,再求S4
(2)根据S1,S2,S3成等比数列,求出d=0或a1=
d,再分别判断数列{Sn}是否成等比数列
(2)根据S1,S2,S3成等比数列,求出d=0或a1=
| 3 |
| 2 |
解答:
解:(1)当a1=3,d=2时,an=2n+1,
∵Sn=a 2n-1+a 2n-1+1+…+a 2n-1,
∴S4=a8+a9+…+a15=
=192;
(2)∵S1,S2,S3成等比数列,
∴S1=a1≠0,S1S3=S22,
∴a1(4a1+18d)=(2a1+3d)2,
∴d=0或a1=
d.
d=0时,
=2,数列{Sn}成等比数列;
a1=
d时,Sn=a 2n-1+a 2n-1+1+…+a 2n-1=2n-1a 2n-1+
d=
d•4n-1≠0,
∴
=4,数列{Sn}成等比数列.
∵Sn=a 2n-1+a 2n-1+1+…+a 2n-1,
∴S4=a8+a9+…+a15=
| 8(17+31) |
| 2 |
(2)∵S1,S2,S3成等比数列,
∴S1=a1≠0,S1S3=S22,
∴a1(4a1+18d)=(2a1+3d)2,
∴d=0或a1=
| 3 |
| 2 |
d=0时,
| Sn+1 |
| Sn |
a1=
| 3 |
| 2 |
| 2n-1(2n-1-1) |
| 2 |
| 3 |
| 2 |
∴
| Sn+1 |
| Sn |
点评:本题考查等比数列的性质,考查等比数列的判断,正确求和是关键.

练习册系列答案
相关题目
执行如图所示的程序框图,如果输入a=2,那么输出的结果为( )


| A、2 | B、3 | C、4 | D、5 |
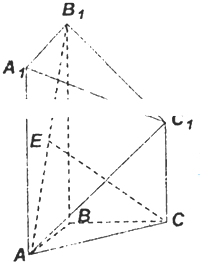 如图,在几何体ABC-A1B1C1中,点A1、B1、C1在平面ABC内的正投影分别为A、B、C,且AB⊥BC,AA1=BB1=4,AB=BC=CC1=2,E为AB1的中点.
如图,在几何体ABC-A1B1C1中,点A1、B1、C1在平面ABC内的正投影分别为A、B、C,且AB⊥BC,AA1=BB1=4,AB=BC=CC1=2,E为AB1的中点. 如图,设点P在曲线y=x2,从原点向A(2,4)移动,让直线OP与曲线y=x2所围成图形面积为S1,直线OP、直线x=2与曲线y=x2所围成图形的面积为S2.
如图,设点P在曲线y=x2,从原点向A(2,4)移动,让直线OP与曲线y=x2所围成图形面积为S1,直线OP、直线x=2与曲线y=x2所围成图形的面积为S2.