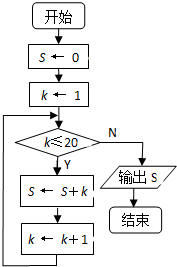
题目内容

若定积分
∫
a
0
|x-1|dx=
2
3
，则a=
 
．
考点：定积分
专题：导数的概念及应用
分析：利用分段函数，需要讨论a与1的关系，去掉绝对值，再根据微积分基本定理求得．
解答： 解：当a＞1时，
∫
a
0
|x-1|dx=
∫
1
0
(1-x)dx+
∫
a
1
(x-1)dx=(x-
1
2
x2)
|
1
0
+(
1
2
x2-x)
|
a
1
=
1
2
a2-a+1，
∴
1
2
a2-a+1=
2
3
，
解得，a=
3+
3
3
，
当0＜a≤1时，
∫
a
0
|x-1|dx=
∫
a
0
(1-x)dx+
∫
1
a
(x-1)dx=(x-
1
2
x2)
|
a
0
+(
1
2
x2-x)
|
1
a
=-a2+2a-
1
2
，
∴-a2+2a-
1
2
=
2
3

即(a-1)2=-
1
6

∴该方程无解．
故答案为：
3+
3
3
点评：本题主要考查了微积分基本定理，关键是对于参数a要分类讨论，属于中档题．
练习册系列答案
相关题目
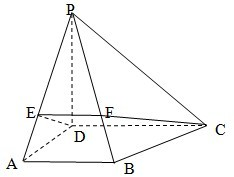已知四棱锥P-ABCD，PD⊥面ABCD，AB∥DC，AD⊥DC，AD=
2
，CD=4，PD=2，E为AP上一点，DE⊥AP，F是平面DEC与BP的交点．
（Ⅰ）求证：EF∥AB；
（Ⅱ）求证：AP⊥面EFCD；
（Ⅲ）求PC与面EFCD所成角的正弦值．
已知函数f（x）=-
1
3
x3+
a
2
x2-2x，g（x）=
1
3
x3-
a
2
x2+（a+2）x+
a+1
x
-lnx，（a∈R）
（Ⅰ）当a=3时，x∈[
3
2
，2]，求函数f（x）的最大值；
（Ⅱ）当a≥-1时，讨论函数F（x）=f（x）+g（x）的单调性；
（Ⅲ）若过点（0，-
1
3
）可作函数y=f（x）图象的三条不同切线，求实数a的取值范围．
∫
4
0
16-x2
dx=
 
．
设f（x）=3-|x-1|，则
∫
2
-2
f（x）dx=
 
．
执行如图的流程图，输出的S=
 
．
从装有n+1个球（其中n个白球，1个黑球）的口袋中取出m个球（0＜m≤n，m，n∈N），共有
C
m
n+1
种取法．在这
C
m
n+1
种取法中，可以分成两类：一类是取出的m个球全部为白球，共有C
 
0
1
•C
 
m
n
+C
 
1
1
•C
 
m-1
n
=C
 
0
1
•C
 
m
n+1
，即有等式：C
 
m
n
+C
 
m-1
n
=C
 
m
n+1
成立．试根据上述思想化简下列式子：C
 
m
n
+C
 
1
k
•C
 
m-1
n
+C
 
2
k
•C
 
m-2
n
+…+C
 
k
k
•C
 
m-k
n
=
 
（1≤k＜m≤n，k，m，n∈N）．
已知A、B是抛物线y2=4x上两点，F是抛物线的焦点，O是平面直角坐标系的原点，若S△AOF•S△BOF=1，则
OA
•
OB
=
 
．
已知函数f（x）=
1-x
ax
+lnx（a＞0），若函数f（x）在区间（1，+∞）上为增函数，则正实数a的取值范围是
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网