题目内容
数列{an}的通项公式为an=20-3n.
(1)证明数列{an}是等差数列;
(2)求{|an|}的前n项和Tn.
(1)证明数列{an}是等差数列;
(2)求{|an|}的前n项和Tn.
考点:数列的求和,等差关系的确定
专题:等差数列与等比数列
分析:(1)根据数列的通项公式结合等差数列的定义证明;
(2)求出等差数列的前6项大于0,自第7项后小于0,当n≤6时数列{|an|}的前n项和即为等差数列{an}的前n项和,当n>6时由等差数列{an}的前n项和的负值加上2倍等差数列的前6项和得答案.
(2)求出等差数列的前6项大于0,自第7项后小于0,当n≤6时数列{|an|}的前n项和即为等差数列{an}的前n项和,当n>6时由等差数列{an}的前n项和的负值加上2倍等差数列的前6项和得答案.
解答:
(1)证明:∵an=20-3n,
∴an+1=20-3(n+1),
则an+1-an=20-3(n+1)-20+3n=-3为常数.
∴数列{an}是等差数列;
(2)由an=20-3n>0,得n<
,
由n∈N*,得n=1,2,3,4,5,6.
∴数列{an}的前6项大于0,自第7项后小于0.
又a1=17,d=-3.
则当n≤6时,{|an|}的前n项和Tn=na1+
=17n-
=-
+
;
当n>6时,{|an|}的前n项和Tn=-(-
+
)+2S6
=
-
+2×(6×17-
)=
-
+114.
∴Tn=
.
∴an+1=20-3(n+1),
则an+1-an=20-3(n+1)-20+3n=-3为常数.
∴数列{an}是等差数列;
(2)由an=20-3n>0,得n<
| 20 |
| 3 |
由n∈N*,得n=1,2,3,4,5,6.
∴数列{an}的前6项大于0,自第7项后小于0.
又a1=17,d=-3.
则当n≤6时,{|an|}的前n项和Tn=na1+
| n(n-1)d |
| 2 |
| 3n(n-1) |
| 2 |
| 3n2 |
| 2 |
| 37n |
| 2 |
当n>6时,{|an|}的前n项和Tn=-(-
| 3n2 |
| 2 |
| 37n |
| 2 |
=
| 3n2 |
| 2 |
| 37n |
| 2 |
| 6×5×3 |
| 2 |
| 3n2 |
| 2 |
| 37n |
| 2 |
∴Tn=
|
点评:本题考查了等差关系的确定,考查了数列前n项和的求法,体现了分类讨论的数学思想方法,是中档题.

练习册系列答案
相关题目
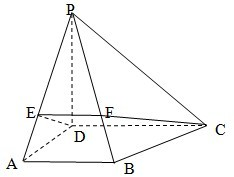 已知四棱锥P-ABCD,PD⊥面ABCD,AB∥DC,AD⊥DC,AD=
已知四棱锥P-ABCD,PD⊥面ABCD,AB∥DC,AD⊥DC,AD=