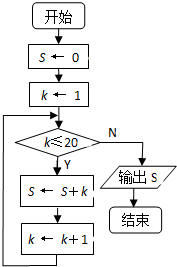
题目内容
已知椭圆E:
+
=1(a>b>0)的离心率为
,且经过点(1,
).
(1)求椭圆E的方程;
(2)O为坐标原点,直线y=kx+m与椭圆E相交于不同的两点A、B,若椭圆E上存在点C,使得O为△ABC的重心,试探究△ABC的面积是否为定值?若是,求出这个定值,若不是,说明理由.
| x2 |
| a2 |
| y2 |
| b2 |
| 1 |
| 2 |
| 3 |
| 2 |
(1)求椭圆E的方程;
(2)O为坐标原点,直线y=kx+m与椭圆E相交于不同的两点A、B,若椭圆E上存在点C,使得O为△ABC的重心,试探究△ABC的面积是否为定值?若是,求出这个定值,若不是,说明理由.
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(1)由已知条件推导出
,由此能求出椭圆方程.
(2)设直线AB方程为:y=kx=m,由
,得(3+4k2)x2+8kmx+4m2-12=0,由此利用韦达定理、三角形重心坐标公式结合已知条件能证明△ABC的面积为定值
.
|
(2)设直线AB方程为:y=kx=m,由
|
| 9 |
| 2 |
解答:
解:(1)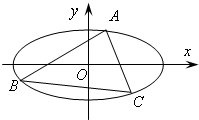 ∵椭圆E:
∵椭圆E:
+
=1(a>b>0)的离心率为
,
且经过点(1,
),
∴
,
解得a=2,b=
,c=1,
∴椭圆方程为
+
=1.…..5 分
(2)设直线AB方程为:y=kx=m,
由
,得(3+4k2)x2+8kmx+4m2-12=0,
∴
,
∵O为重心,
=-(
+
)=(
,
),…..8分
∵C点在椭圆E上,∴
+
=1,
解得4m2=4k2+3,…..10分
∵|AB|=
•
=
•
,…12分
∴S△ABC=
|AB|d=
=
.…14分
直线AB斜率不存在时,|AB|=2,d=3,S△ABC=
.
△ABC的面积为定值
.
 ∵椭圆E:
∵椭圆E:| x2 |
| a2 |
| y2 |
| b2 |
| 1 |
| 2 |
且经过点(1,
| 3 |
| 2 |
∴
|
解得a=2,b=
| 3 |
∴椭圆方程为
| x2 |
| 4 |
| y2 |
| 3 |
(2)设直线AB方程为:y=kx=m,
由
|
∴
|
∵O为重心,
| OC |
| OA |
| OB |
| 8km |
| 3+4k2 |
| -6m |
| 3+4k2 |
∵C点在椭圆E上,∴
(
| ||
| 4 |
(
| ||
| 3 |
解得4m2=4k2+3,…..10分
∵|AB|=
| 1+k2 |
(
|
=
4
| ||
| 3+4k2 |
| 12k2+9-3m2 |
∴S△ABC=
| 1 |
| 2 |
| 6|m| |
| 3+4k2 |
| 12k2+9-3m2 |
| 9 |
| 2 |
直线AB斜率不存在时,|AB|=2,d=3,S△ABC=
| 9 |
| 2 |
△ABC的面积为定值
| 9 |
| 2 |
点评:本题考查椭圆方程的求法,考查三角形面积是否为定值的判断与求法,解题时要认真审题,注意韦达定理的合理运用.

练习册系列答案
相关题目
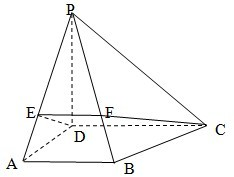 已知四棱锥P-ABCD,PD⊥面ABCD,AB∥DC,AD⊥DC,AD=
已知四棱锥P-ABCD,PD⊥面ABCD,AB∥DC,AD⊥DC,AD=