题目内容
直线l过点(1,1),交x轴,y轴的正半轴分别于A,B,过A,B作直线3x+y+3=0的垂线,垂足分别为C,D.
(1)当AB∥CD时,求CD中点M的坐标;
(2)当|CD|最小时,求直线l的方程.
(1)当AB∥CD时,求CD中点M的坐标;
(2)当|CD|最小时,求直线l的方程.
考点:直线的截距式方程
专题:不等式的解法及应用,直线与圆
分析:(1)直接设截距式方程,代入点的坐标,和AB∥CD斜率相等的条件,可确定方程,设出AB的中点N,求出MN的方程与CD的方程联立解得点M的坐标;
(2)利用点到直线的距离公式表示出|CD|,利用基本不等式求解即可
(2)利用点到直线的距离公式表示出|CD|,利用基本不等式求解即可
解答:
解:依题意,设A(a,0),B(0,b),a>0,b>0,
则直线AB的方程为
+
=1,
∵点(1,1)在AB上,∴
+
=1,①
(1)当AB∥CD时,则可得kAB=-3,
即-
=-3∴b=3a
结合①解得a=
,b=4
设AB的中点为N,则N(
,2).
又∵AC,BD⊥垂直于CD,M是CD的中点∴MN⊥CD,
从而直线MN的方程为y=
(x-
)+2
与方程3x+y+3=0联立,
可解得M(-
,
)
(2)∵AC,BD⊥垂直于直线y=-3x-3,
∴直线AC的方程为y=
(x-a),即x-3y-a=0,
且点B到直线AC的距离就等于|CD|,
故得|CD|=
=
(
+
)
=
(4+
+
)≥
(4+2
)
当且仅当
即
等号成立
因此,所求的直线l的方程为x+
y-
-1=0.
则直线AB的方程为
| x |
| a |
| y |
| b |
∵点(1,1)在AB上,∴
| 1 |
| a |
| 1 |
| b |
(1)当AB∥CD时,则可得kAB=-3,
即-
| b |
| a |
结合①解得a=
| 4 |
| 3 |
设AB的中点为N,则N(
| 1 |
| 3 |
又∵AC,BD⊥垂直于CD,M是CD的中点∴MN⊥CD,
从而直线MN的方程为y=
| 1 |
| 3 |
| 2 |
| 3 |
与方程3x+y+3=0联立,
可解得M(-
| 43 |
| 30 |
| 13 |
| 10 |
(2)∵AC,BD⊥垂直于直线y=-3x-3,
∴直线AC的方程为y=
| 1 |
| 3 |
且点B到直线AC的距离就等于|CD|,
故得|CD|=
| |-3b-a| | ||
|
| a+3b | ||
|
| 1 |
| a |
| 1 |
| b |
=
| 1 | ||
|
| 3b |
| a |
| a |
| b |
| 1 | ||
|
| 3 |
当且仅当
|
|
因此,所求的直线l的方程为x+
| 3 |
| 3 |
点评:本题主要考查了直线的截距式方程应用,直线平行和垂直的性质,以及距离公式和基本不等式的综合应用.属于难题.

练习册系列答案
 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
问题:①有1000盒生产批次不同的药品,第一批500盒,第二批200盒,第三批300盒,现从中抽取一个容量为100的样本;②从20名学生中选出3名参加座谈会.方法:1.简单随机抽样法;2.系统抽样法;3.分层抽样法.其中问题与方法的最佳配对是( )
| A、①1,②2 |
| B、①3,②1 |
| C、①2,②3 |
| D、①3,②2 |
已知双曲线
-
=1的一个焦点与抛物线y2=-4x的焦点重合,且双曲线的离心率为
,则此双曲线的方程为( )
| x2 |
| a2 |
| y2 |
| b2 |
| 5 |
A、5x2-
| ||||
B、5x2-
| ||||
C、
| ||||
D、
|
【文科】如果双曲线的焦距等于两条准线间距离的4倍,则此双曲线的离心率为( )
| A、4 | ||
B、
| ||
C、
| ||
| D、2 |
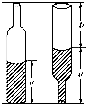 如图,啤酒瓶的高为h,瓶内酒面高度为a,若将瓶盖盖好倒置,酒面高度为a′(a′+b=h),则酒瓶容积与瓶内酒的体积之比为( )
如图,啤酒瓶的高为h,瓶内酒面高度为a,若将瓶盖盖好倒置,酒面高度为a′(a′+b=h),则酒瓶容积与瓶内酒的体积之比为( )A、1+
| ||
B、1+
| ||
C、1+
| ||
D、1+
|