题目内容
若函数f(x)=x2+ax+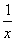 在
在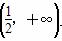 上是增函数,则a的取值范围是( )
上是增函数,则a的取值范围是( )
A.[-1,0] B.[-1,+∞)
C.[0,3] D.[3,+∞)
D

练习册系列答案
 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案
相关题目
题目内容
若函数f(x)=x2+ax+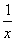 在
在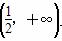 上是增函数,则a的取值范围是( )
上是增函数,则a的取值范围是( )
A.[-1,0] B.[-1,+∞)
C.[0,3] D.[3,+∞)
D

 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案