题目内容
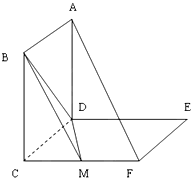 如图,正方形 ABCD 和正方形 CDEF所在平面互相垂直,M为FC的中点.
如图,正方形 ABCD 和正方形 CDEF所在平面互相垂直,M为FC的中点.(1)求证:AF∥平面MBD;
(2)求异面直线AF与BM所成角的余弦值.
考点:异面直线及其所成的角,直线与平面平行的判定
专题:空间位置关系与距离
分析:(1)连接AC,BD交于点O,连接MO,可得△ACF中,MO为中位线,即MO∥AF,进而由线面平行的判定定理可得AF∥平面MBD;
(2)由(1)中MO∥AF,可得AF与BM所成角即∠OMB,解三角形可得:异面直线AF与BM所成角的余弦值.
(2)由(1)中MO∥AF,可得AF与BM所成角即∠OMB,解三角形可得:异面直线AF与BM所成角的余弦值.
解答:
 证明:(1)连接AC,BD交于点O,连接MO
证明:(1)连接AC,BD交于点O,连接MO
∵ABCD为正方形,
∴O为AC中点
∵△ACF中,M为EC中点
∴MO∥AF
又∵MO?平面MBD,AF?平面MBD,
∴AF∥平面MBD.
(2)解:根据(1)得AF∥OM,
AF与BM所成角即∠OMB,
设正方形边长为a,
则AC=
a,AF=
a,MO=
AF=
a,MC=
a
∴MB=
=
a
∴cos∠BMO=
=
=
.
 证明:(1)连接AC,BD交于点O,连接MO
证明:(1)连接AC,BD交于点O,连接MO ∵ABCD为正方形,
∴O为AC中点
∵△ACF中,M为EC中点
∴MO∥AF
又∵MO?平面MBD,AF?平面MBD,
∴AF∥平面MBD.
(2)解:根据(1)得AF∥OM,
AF与BM所成角即∠OMB,
设正方形边长为a,
则AC=
| 2 |
| 3 |
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
∴MB=
| MC2+CB2 |
| ||
| 2 |
∴cos∠BMO=
| MO |
| MB |
| ||||
|
| ||
| 5 |
点评:本题考查的知识点是异面直线及其所成的角,直线与平面平行的判定,难度中档.

练习册系列答案
相关题目
若命题“p∧q”是假命题,则( )
| A、p∨q为假命题 |
| B、(?p)∨(?q)为真命题 |
| C、(?p)∨(?q)为假命题 |
| D、p∨q为真命题 |
已知点M(a,b)(a>0,b>0)是圆C:x2+y2=1内任意一点,点P(x,y)是圆上任意一点,则实数ax+by-1为( )
| A、一定是负数 | B、一定等于0 |
| C、一定是正数 | D、不确定 |
 在斜棱柱ABC-A1B1C1中,D为AC的中点,求证:AB1∥平面BC1D.
在斜棱柱ABC-A1B1C1中,D为AC的中点,求证:AB1∥平面BC1D.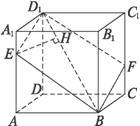 如图,正方体ABCD-A1B1C1D1的棱长为a,过其对角线BD1的平面分别与AA1、CC1相交于点E,F,求截面四边形BED1F面积的最小值.
如图,正方体ABCD-A1B1C1D1的棱长为a,过其对角线BD1的平面分别与AA1、CC1相交于点E,F,求截面四边形BED1F面积的最小值. 正方形ADEF与梯形ABCD所在平面互相垂直,AD⊥CD,AB∥CD,AB=AD=
正方形ADEF与梯形ABCD所在平面互相垂直,AD⊥CD,AB∥CD,AB=AD=