题目内容
已知:cos2α+cos2β=
,则cos(α+β)cos(α-β)的值是 .
| 4 |
| 5 |
考点:两角和与差的余弦函数
专题:三角函数的求值
分析:利用两角和与差的余弦展开,然后代入cos2α+cos2β=
得答案.
| 4 |
| 5 |
解答:
解:∵cos2α+cos2β=
,
∴cos(α+β)cos(α-β)=(cosαcosβ-sinαsinβ)(cosαcosβ+sinαsinβ)
=cos2αcos2β-sin2αsin2β=cos2αcos2β-(1-cos2α)(1-cos2β)
=cos2αcos2β-1+(cos2α+cos2β)-cos2αcos2β
=-1+cos2α+cos2β=-1+
=-
.
故答案为:-
.
| 4 |
| 5 |
∴cos(α+β)cos(α-β)=(cosαcosβ-sinαsinβ)(cosαcosβ+sinαsinβ)
=cos2αcos2β-sin2αsin2β=cos2αcos2β-(1-cos2α)(1-cos2β)
=cos2αcos2β-1+(cos2α+cos2β)-cos2αcos2β
=-1+cos2α+cos2β=-1+
| 4 |
| 5 |
| 1 |
| 5 |
故答案为:-
| 1 |
| 5 |
点评:本题考查了两角和与差的余弦,是基础的计算题.

练习册系列答案
相关题目
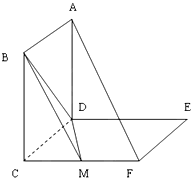 如图,正方形 ABCD 和正方形 CDEF所在平面互相垂直,M为FC的中点.
如图,正方形 ABCD 和正方形 CDEF所在平面互相垂直,M为FC的中点.