题目内容
已知，其中i为虚数单位，z1=1+i，z2=2+bi，若z1•z2为实数，则实数b= ．
考点：复数代数形式的乘除运算
专题：数系的扩充和复数
分析：利用复数的运算法则、复数为实数的充要条件即可得出．
解答：
解：z1•z2=（1+i）（2+bi）=2-b+（2+b）i为实数，
∴2+b=0，解得b=-2．
故答案为：-2．
∴2+b=0，解得b=-2．
故答案为：-2．
点评：本题考查了复数的运算法则、复数为实数的充要条件，属于基础题．
练习册系列答案
相关题目
已知向量
=（1，2x），
=（4，-x），则“x=
”是“
⊥
”的（ ）
| a |
| b |
| 2 |
| a |
| b |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
已知△ABC的三边长a=3，b=4，c=
，则该三角形的最大内角为（ ）
| 37 |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知R为实数集，A={x|2x-3＜3x}，B={x|x≥2}，则A∪B=（ ）
| A、{x|x≥2} |
| B、{x|x＞-3} |
| C、{x|2≤x＜3} |
| D、R |
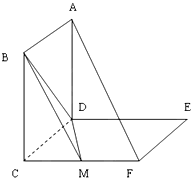如图，正方形 ABCD 和正方形 CDEF所在平面互相垂直，M为FC的中点．