Question

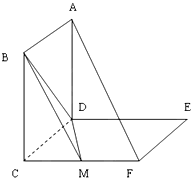
正方形ADEF与梯形ABCD所在平面互相垂直，AD⊥CD，AB∥CD，AB=AD=

1

2

CD=2，点M在线段EC上且不与E，C重合．
（Ⅰ）当点M是EC中点时，求证：BM∥平面ADEF；
（Ⅱ）当平面BDM与平面ABF所成锐二面角的余弦值为

6

6

时，求三棱锥M-BDE的体积．

Answer 1

考点：棱柱、棱锥、棱台的体积,直线与平面平行的判定

专题：空间位置关系与距离,空间角

分析：（I）三角形的中位线定理可得MN∥DC，MN=

1

2

DC．再利用已知可得MN

∥

.

BA，即可证明四边形ABMN是平行四边形．再利用线面平行的判定定理即可证明．
（II）取CD的中点O，过点O作OP⊥DM，连接BP．可得四边形ABOD是平行四边形，由于AD⊥DC，可得四边形ABOD是矩形．由于BO⊥CD，正方形ADEF与梯形ABCD所在平面互相垂直，ED⊥AD，可得ED⊥平面ADCB，平面CDE⊥平面ADCB．BO⊥平面CDE．于是BP⊥DM．即可得出∠OPB是平面BDM与平面ABF（即平面ABF）所成锐二面角．由于cos∠OPB=

6

6

，可得BP=

2 30

5

．可得sin∠MDC=

OP

OD

=

5

5

．而sin∠ECD=

2

2 5

=

5

5

．而DM=MC，同理DM=EM．M为EC的中点，利用三棱锥的体积计算公式可得V_M-BDE=V_B-DEM=

1

3

S△DEM•AD．

解答： （I）证明：取ED的中点N，连接MN．
又∵点M是EC中点．
∴MN∥DC，MN=

1

2

DC．
而AB∥DC，AB=

1

2

DC．
∴MN

∥

.

BA，
∴四边形ABMN是平行四边形．
∴BM∥AN．
而BM?平面ADEF，AN?平面ADEF，
∴BM∥平面ADEF．
（Ⅱ）取CD的中点O，过点O作OP⊥DM，连接BP．
∵AB∥CD，AB=

1

2

CD=2，
∴四边形ABOD是平行四边形，
∵AD⊥DC，
∴四边形ABOD是矩形．
∴BO⊥CD．
∵正方形ADEF与梯形ABCD所在平面互相垂直，ED⊥AD，
∴ED⊥平面ADCB．
∴平面CDE⊥平面ADCB．
∴BO⊥平面CDE．
∴BP⊥DM．
∴∠OPB是平面BDM与平面ABF（即平面ABF）所成锐二面角．
∵cos∠OPB=

6

6

，∴sin∠OPB=

30

6

．
∴

OP

BP

=

30

6

，解得BP=

2 30

5

．
∴OP=BPcos∠OPB=

2 5

5

．
∴sin∠MDC=

OP

OD

=

5

5

．
而sin∠ECD=

2

2 5

=

5

5

．
∴DM=MC，同理DM=EM．
∴M为EC的中点，
∴

S

△DEM

=

1

2

S

△CDE

=2，
∵AD⊥CD，AD⊥DE，且DE与CD相交于D
∴AD⊥平面CDE．
∵AB∥CD，
∴三棱锥B-DME的高=AD=2，
∴V_M-BDE=V_B-DEM=

1

3

S△DEM•AD=

4

3

．

点评：本题考查了三角形的中位线定理、梯形的定义、平行四边形的判定与性质定理、线面平行的判定定理、线面面面垂直的判定与性质定理、二面角的作法与应用、三棱锥的体积计算公式，考查了空间想象能力，考查了推理能力与计算能力，属于难题．