题目内容
在斜棱柱ABC-A1B1C1中，D为AC的中点，求证：AB1∥平面BC1D．考点：直线与平面平行的判定
专题：空间位置关系与距离
分析：连接B1C交BC1于点O，连接OD，则点O为B1C的中点．可得DO为△AB1C中位线，A1B∥OD，结合线面平行的判定定理，证得A1B∥平面BC1D；
解答：
证明：设B1C交BC1于点O，连接OD，则点O为B1C的中点．
∵D为AC中点，得DO为△AB1C中位线，
∴A1B∥OD．
∵OD?平面AB1C，A1B?平面AB1C，
∴直线AB1∥平面BC1D．
证明：设B1C交BC1于点O，连接OD，则点O为B1C的中点．∵D为AC中点，得DO为△AB1C中位线，
∴A1B∥OD．
∵OD?平面AB1C，A1B?平面AB1C，
∴直线AB1∥平面BC1D．
点评：本题主要考查了空间线面平行的判定定理的应用，其中，设B1C交BC1于点O，连接OD，是解题的关键，属于基础题．
练习册系列答案
相关题目
如图所示，AB为⊙O的直径，C为⊙O上一点，PA⊥平面ABC，AE⊥PB，垂足为E，AF⊥Pc，垂足为F，求证：PB⊥平面AEF．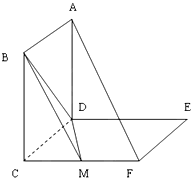
如图，正方形 ABCD 和正方形 CDEF所在平面互相垂直，M为FC的中点．