题目内容
20.虚数(x-2)+yi,其中x、y均为实数,当此虚数的模为1时,$\frac{y}{x}$的取值范围是$[{-\frac{{\sqrt{3}}}{3},0})∪({0,\frac{{\sqrt{3}}}{3}}]$.分析 $\sqrt{(x-2)^{2}+{y}^{2}}$=1,即(x-2)2+y2=1,y≠0.设$\frac{y}{x}$=k≠0,即y=kx.可得$\frac{|2k|}{\sqrt{1+{k}^{2}}}$<1,解得k范围.
解答 解:∵$\sqrt{(x-2)^{2}+{y}^{2}}$=1,即(x-2)2+y2=1,y≠0.
设$\frac{y}{x}$=k≠0,即y=kx.
∴$\frac{|2k|}{\sqrt{1+{k}^{2}}}$<1,解得:$-\frac{\sqrt{3}}{3}$≤k≤$\frac{\sqrt{3}}{3}$,k≠0.
故答案为:$[{-\frac{{\sqrt{3}}}{3},0})∪({0,\frac{{\sqrt{3}}}{3}}]$.
点评 本题考查了虚数的定义、直线与圆的位置关系、点到直线的距离公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 同步奥数系列答案
同步奥数系列答案
相关题目
10.在用二分法求方程零点的算法中,下列说法正确的是( )
| A. | 这个算法可以求方程所有的零点 | |
| B. | 这个算法可以求任何方程的零点 | |
| C. | 这个算法能求方程所有的近似零点 | |
| D. | 这个算法并不一定能求方程所有的近似零点 |
15.函数$y=\sqrt{16-{4}^{x}}$的值域是( )
| A. | (0,4) | B. | (-∞,4) | C. | (4,+∞) | D. | [0,4) |
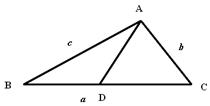 如图,设△ABC的内角A,B,C所对边的长分别是a,b,c,A=$\frac{3π}{4}$,c=6,b=3$\sqrt{2}$,点D在BC边上,且AD=BD,求AD的长.
如图,设△ABC的内角A,B,C所对边的长分别是a,b,c,A=$\frac{3π}{4}$,c=6,b=3$\sqrt{2}$,点D在BC边上,且AD=BD,求AD的长.