Question

8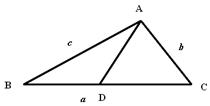．如图，设△ABC的内角A，B，C所对边的长分别是a，b，c，A=$\frac{3π}{4}$，c=6，b=3$\sqrt{2}$，点D在BC边上，且AD=BD，求AD的长．

Answer 1

分析 由已知及余弦定理可解得BC的值，由正弦定理可求得sinB，从而可求cosB，过点D作AB的垂线DE，垂足为E，由AD=BD得：cos∠DAE=cosB，即可求得AD的长．

解答 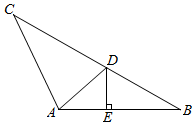解：∵A=$\frac{3π}{4}$，c=6，b=3$\sqrt{3}$，
∴在△ABC中，由余弦定理可得：a²=b²+c²-2b•ccos∠BAC=90．
∴a=3$\sqrt{10}$，
∵在△ABC中，由正弦定理可得：$\frac{b}{sinB}$=$\frac{a}{sin∠BAC}$，
∴sinB=$\frac{\sqrt{10}}{10}$，
∴cosB=$\sqrt{1-si{n}^{2}B}$=$\frac{3\sqrt{10}}{10}$，
∵过点D作AB的垂线DE，垂足为E，由AD=BD，得：cos∠DAE=cosB，
∴Rt△ADE中，AD=$\frac{AE}{cos∠DAE}$=$\frac{3}{cosB}$=$\sqrt{10}$．
AD的长$\sqrt{10}$．

点评 本题主要考查了正弦定理，余弦定理在解三角形中的应用，考查了计算能力和转化思想，属于基本知识的考查，属于中档题．