题目内容
9.等差数列{an}中,S3=12,a5=2a2-1.(Ⅰ)求数列的通项公式an;
(Ⅱ)求数列{$\frac{{a}_{n+2}-{a}_{n}}{a{{\;}_{n}a}_{n+2}}$}的前n(n≥2)项和Sn.
分析 (Ⅰ)设公差为d,根据题意可得关于a1,d的方程组,求出a1,d,即可求出通项公式,
(Ⅱ)根据裂项求和即可.
解答 解:(Ⅰ)等差数列{an}中,S3=12,a5=2a2-1,
设公差为d,则$\left\{\begin{array}{l}{3{a}_{1}+3d=12}\\{{a}_{1+}4d=2{a}_{1}+2d-1}\end{array}\right.$,
解得a1=3,d=1,
∴an=a1+(n-1)d=3+(n-1)=n+2;
(Ⅱ)$\frac{{a}_{n+2}-{a}_{n}}{a{{\;}_{n}a}_{n+2}}$=$\frac{(n+2)+2-n-2}{(n+2)(n+4)}$=$\frac{2}{(n+2)(n+4)}$=$\frac{1}{n+2}$-$\frac{1}{n+4}$,
∴Sn=$\frac{1}{3}$-$\frac{1}{5}$+$\frac{1}{4}$-$\frac{1}{6}$+…+$\frac{1}{n+1}$-$\frac{1}{n+3}$+$\frac{1}{n+2}$-$\frac{1}{n+4}$=$\frac{1}{3}$+$\frac{1}{4}$-$\frac{1}{n+3}$-$\frac{1}{n+4}$=$\frac{7}{12}$-$\frac{1}{n+3}$-$\frac{1}{n+4}$.
点评 本题考查了等差数列的通项公式和求和公式,以及裂项求和,属于中档题

练习册系列答案
相关题目
4.已知A,B,C三点在球O的表面,△ABC是边长为5正三角形,球面上另外一点D到A,B,C三点的距离分别是3,4,5,则球O的表面积是( )
| A. | $\frac{100π}{3}$ | B. | $\frac{400π}{3}$ | C. | 100π | D. | 400π |
19.某市电子认证审查流程图如图:
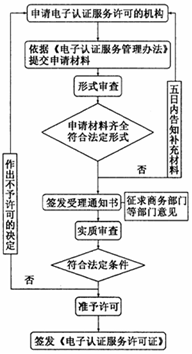
则有几处审查可能不被通过的环节( )

则有几处审查可能不被通过的环节( )
| A. | 1 | B. | 2 | C. | 3 | D. | 0 |