题目内容
10.在平面直角坐标系xoy中,直线l的参数方程为$\left\{\begin{array}{l}x=tcosα\\ y=1+tsinα\end{array}\right.$(t为参数),以坐标原点O为极点,x轴的正半轴为极轴的极坐标系中,曲线C的极坐标方程为ρcos2θ=4sinθ.(1)设M(x,y)为曲线C上的任意一点,求x+y的取值范围;
(2)若直线l与曲线C交于A,B两点,求|AB|的最小值.
分析 (1)把x=ρcosθ,y=ρsinθ代入曲线C的极坐标方程化直角坐标方程,利用x+y=x+$\frac{1}{4}{x}^{2}$=$\frac{1}{4}(x+2)^{2}$-1,即可得出结论;
(2)将直线的参数方程代入曲线C的直角坐标方程,利用根与系数的关系结合t的几何意义求得|AB|的最小值.
解答 解:(1)由ρcos2θ=4sinθ,得(ρcosθ)2=4ρsinθ,
把x=ρcosθ,y=ρsinθ代入上式,得x2=4y,
∴曲线C的直角坐标方程为x2=4y,
∵M(x,y)为曲线C上的任意一点,
∴x+y=x+$\frac{1}{4}{x}^{2}$=$\frac{1}{4}(x+2)^{2}$-1≥-1,
∴x+y的取值范围是[-1,+∞);
(2)将直线l的参数方程代入x2=4y,得t2cos2α-4tsinα-4=0,
设A、B两点对应的参数分别为t1,t2,
则|AB|=|t1-t2|=$\frac{4}{co{s}^{2}α}$,当cos2α=1时,|AB|的最小值为4.
点评 本题考查极坐标方程化直角坐标方程,考查直线参数方程中参数几何意义的应用,是基础题.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
5.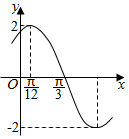 函数$f(x)=Asin({ωx+ϕ})({A>0,ω>0,|φ|<\frac{π}{2}})$的部分图象如图所示,
函数$f(x)=Asin({ωx+ϕ})({A>0,ω>0,|φ|<\frac{π}{2}})$的部分图象如图所示,
求(Ⅰ)函数f(x)的解析式;
(Ⅱ)函数y=Acos(ωx+ϕ)的单调递增区间.
 函数$f(x)=Asin({ωx+ϕ})({A>0,ω>0,|φ|<\frac{π}{2}})$的部分图象如图所示,
函数$f(x)=Asin({ωx+ϕ})({A>0,ω>0,|φ|<\frac{π}{2}})$的部分图象如图所示,求(Ⅰ)函数f(x)的解析式;
(Ⅱ)函数y=Acos(ωx+ϕ)的单调递增区间.
2.已知$sin(-α)=\frac{{\sqrt{5}}}{3}$,则$cos(\frac{π}{2}+α)$的值为( )
| A. | $\frac{2}{3}$ | B. | $-\frac{2}{3}$ | C. | $\frac{{\sqrt{5}}}{3}$ | D. | $-\frac{{\sqrt{5}}}{3}$ |
19.某市电子认证审查流程图如图:
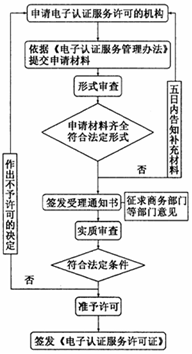
则有几处审查可能不被通过的环节( )

则有几处审查可能不被通过的环节( )
| A. | 1 | B. | 2 | C. | 3 | D. | 0 |
20.等差数列{an}中,a1=2,公差d=3则{an}的通项公式为( )
| A. | .an=3n-1 | B. | an=2n+1 | C. | .an=2n+3 | D. | .an=3n+2 |