题目内容
已知f（x）是定义在R上的奇函数，当x≥0时，f（x）=-x2+2x，求f（x）的解析式．
考点：函数解析式的求解及常用方法,函数奇偶性的性质
专题：函数的性质及应用
分析：设x＜0，则-x＞0，结合已知可得此时函数的解析式，综合可得．
解答：
解：设x＜0，则-x＞0，
∵当x≥0时，f（x）=-x2+2x，
∴f（-x）=-x2-2x，
又f（x）是定义在R上的奇函数，
∴f（-x）=-f（x），
∴-f（x）=-x2-2x，
∴f（x）=x2+2x，
∴f（x）=
∵当x≥0时，f（x）=-x2+2x，
∴f（-x）=-x2-2x，
又f（x）是定义在R上的奇函数，
∴f（-x）=-f（x），
∴-f（x）=-x2-2x，
∴f（x）=x2+2x，
∴f（x）=
|
点评：本题考查函数解析式的求解，涉及函数的奇偶性，属基础题．
练习册系列答案
相关题目
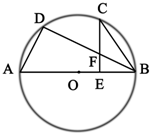如图：AB是⊙O的直径，C是弧BD的中点，CE⊥AB，垂足为E，BD交CE于点F．