题目内容
19.“m>0,n>0”是“$\frac{{x}^{2}}{m}$+$\frac{{y}^{2}}{n}$=1为椭圆方程”的( )| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
分析 利用椭圆的性质求解.
解答 解:∵m>0,n>0,推导不出$\frac{{x}^{2}}{m}$+$\frac{{y}^{2}}{n}$=1为椭圆方程,
$\frac{{x}^{2}}{m}$+$\frac{{y}^{2}}{n}$=1为椭圆方程⇒m>0,n>0,
∴“m>0,n>0”是“$\frac{{x}^{2}}{m}$+$\frac{{y}^{2}}{n}$=1为椭圆方程”的必要不充分条件.
故选:B.
点评 本题考查充分不必要条件、必要不充分条件、充要条件、不充分不必要条件的判断,是基础题,解题时要认真审题,注意椭圆性质的合理运用.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
4.已知函数f(x)在区间[a,b]上单调,且图象是连续不断的,若f(a)•f(b)<0,则方程f(x)=0在区间[a,b]上( )
| A. | 至少有一实根 | B. | 至多有一实根 | C. | 没有实根 | D. | 必有唯一的实根 |
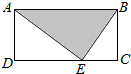 在长方形ABCD中,AB=3,BC=2,E为CD上一点,将一个质点随机投入长方形中,则质点落在阴影部分的概率为$\frac{1}{2}$.
在长方形ABCD中,AB=3,BC=2,E为CD上一点,将一个质点随机投入长方形中,则质点落在阴影部分的概率为$\frac{1}{2}$.