题目内容

9．已知球O的大圆面积为S1，表面积为S2，则S1：S2=1：4．

分析 利用球的面积公式，直接求解即可．

解答 解：设球的半径为r，所以大圆面积S1=πr2，表面积S2=4πr2，
所以S1：S2=1：4
故答案为：1：4．

点评 本题考查球的表面积，考查计算能力，是基础题．

练习册系列答案
相关题目
19．曲线y=$\frac{1}{4}$x2和它在点（2，1）处的切线与x轴围成的封闭图形的面积为$\frac{1}{6}$．
20．${（{\sqrt{x}-\frac{1}{x}}）^5}$的二项展开式中x项的系数为-5．（用数字作答）
17．函数f（x）=sin（ωx+φ）（ω＞0）的一段图象如图所示，则ω=（　　）
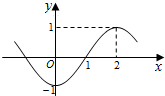
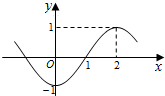
A．$\frac{1}{4}$B．$\frac{1}{2}$C．$\frac{π}{4}$D．$\frac{π}{2}$
4．若α∈（-$\frac{π}{2}$，0），cosα=$\frac{\sqrt{5}}{5}$，则tan（α-$\frac{π}{4}$）=3．
14．已知椭圆C：$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（a＞b＞0）$的离心率为$\frac{{\sqrt{3}}}{2}$，点$A（1，\frac{{\sqrt{3}}}{2}）$在椭圆C上．
（Ⅰ）求椭圆C的方程；
（Ⅱ）设动直线l与椭圆C有且仅有一个公共点，判断是否存在以原点O为圆心的圆，满足此圆与l相交两点P1，P2（两点均不在坐标轴上），且使得直线OP1，OP2的斜率之积为定值？若存在，求此圆的方程；若不存在，说明理由．
1．如果cosθ＜0，且tanθ＞0，则θ是（　　）
A．第一象限的角B．第二象限的角C．第三象限的角D．第四象限的角
18．已知对称轴为坐标轴的双曲线的渐进线方程为y=±$\frac{b}{a}$x（a＞0，b＞0），若双曲线上有一点M（x0，y0），使b|x0|＜a|y0|，则该双曲线的焦点（　　）
A．在x轴上B．在y轴上C．当a＞b时，在x轴上D．当a＞b时，在y轴上
19．“m＞0，n＞0”是“$\frac{{x}^{2}}{m}$+$\frac{{y}^{2}}{n}$=1为椭圆方程”的（　　）
A．充分不必要条件B．必要不充分条件
C．充要条件D．既不充分也不必要条件

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网