题目内容
一个几何体的三视图及尺寸如图所示，则该几何体的体积为（ ）
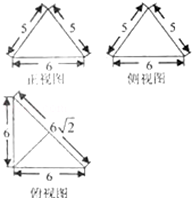
| A、48 | B、72 | C、12 | D、24 |
考点：由三视图求面积、体积
专题：空间位置关系与距离
分析：由已知中三视图可得该几何体为一个以俯视图为底面的三棱锥，求出底面积和高后，代入锥体体积公式，可得答案．
解答：
解：由已知中三视图可得该几何体为一个以俯视图为底面的三棱锥，
其底面面积S=
×6×6=18，
其高h=
=4，
故该几何体的体积V=
Sh=24，
故选：D．
其底面面积S=
| 1 |
| 2 |
其高h=
52-(
|
故该几何体的体积V=
| 1 |
| 3 |
故选：D．
点评：本题考查的知识点是由三视图，求体积，其中根据已知分析出几何体的形状是解答的关键．
练习册系列答案
相关题目
如存在实数x使|x-a|+|x-1|≤3成立，则实数a的取值范围是（ ）
| A、（-2，4） |
| B、[-2，4] |
| C、（-2，3） |
| D、[1，4] |
设曲线y=x3与直线y=x所围成的封闭区域的面积为S，则下列等式成立的是（ ）
A、S=
| ||
B、S=
| ||
C、S=
| ||
D、S=2
|
不等式sin（π+x）＞0成立的x的取值范围为（ ）
| A、（0，π） |
| B、（π，2π） |
| C、（2kπ，2kπ+π）（k∈Z） |
| D、（2kπ+π，2kπ+2π）（k∈Z） |
曲线y=
x3-2在点（1，-
） 处切线的斜率为（ ）
| 1 |
| 3 |
| 5 |
| 3 |
A、
| ||
| B、1 | ||
| C、-1 | ||
D、-
|
由直线y=0，x=e，y=2x及曲线y=
所围成的封闭的图形的面积为（ ）
| 2 |
| x |
| A、3 |
| B、3+2ln2 |
| C、e2-3 |
| D、e |
若复数z满足z=1-2i，则z的虚部为（ ）
| A、-2i | B、2i | C、-2 | D、2 |
若函数f（x）的零点与g（x）=lnx+2x-8的零点之差的绝对值不超过0.5，则f（x）可以是（ ）
| A、f（x）=3x-6 | ||
| B、f（x）=（x-4）2 | ||
| C、f（x）=ex-1-1 | ||
D、f（x）=ln（x-
|