题目内容
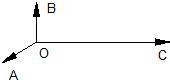 如图,平面内有三个向量
如图,平面内有三个向量| OA |
| OB |
| OC |
| OA |
| OB |
| OA |
| OC |
| OA |
| OB |
| OC |
| 3 |
| OC |
| OA |
| OB |
考点:平面向量数量积的运算,平面向量的基本定理及其意义
专题:平面向量及应用
分析:建立如图所示的直角坐标系,可得点A,B,C的坐标,利用向量的坐标运算和向量相等即可得出.
解答:
解:∵
与
的夹角为120°,
与
的夹角为150°,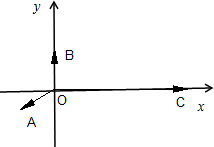
∴向量
与
的夹角为90°.
建立如图所示的直角坐标系.
由于
与
的夹角为120°,|
|=1.
∴A(-
,-
),
又|
|=1,|
|=2
.
∴B(0,1),C(2
,0).
又
=λ
+μ
(λ,μ∈R),
∴(2
,0)=λ(-
,-
)+μ(0,1)=(-
λ,-
λ+μ),
∴
,解得
.
∴λ+μ=-6.
故答案为:-6.
| OA |
| OB |
| OA |
| OC |

∴向量
| OC |
| OB |
建立如图所示的直角坐标系.
由于
| OA |
| OB |
| OA |
∴A(-
| ||
| 2 |
| 1 |
| 2 |
又|
| OB |
| OC |
| 3 |
∴B(0,1),C(2
| 3 |
又
| OC |
| OA |
| OB |
∴(2
| 3 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
∴
|
|
∴λ+μ=-6.
故答案为:-6.
点评:本题考查了向量的坐标运算和向量相等,属于中档题.

练习册系列答案
相关题目
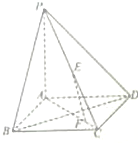 如图,在四棱锥P-ABCD中,底面ABCD是正方形,PA⊥平面ABCD,E是PC中点,F为线段AC上一点.
如图,在四棱锥P-ABCD中,底面ABCD是正方形,PA⊥平面ABCD,E是PC中点,F为线段AC上一点.