题目内容
设正实数x,y满足xy=
,则实数x的最小值为 .
| x+y |
| x-y |
考点:基本不等式
专题:不等式的解法及应用
分析:由正实数x,y满足xy=
,化为xy2+(1-x2)y+x=0,可得
,计算即可.
| x+y |
| x-y |
|
解答:
解:由正实数x,y满足xy=
,
化为xy2+(1-x2)y+x=0,
∴
,化为
,
解得x≥
+1.
因此实数x的最小值为
+1.
故答案为:
+1.
| x+y |
| x-y |
化为xy2+(1-x2)y+x=0,
∴
|
|
解得x≥
| 2 |
因此实数x的最小值为
| 2 |
故答案为:
| 2 |
点评:本题考查了一元二次方程的实数根与判别式、根与系数的关系、一元二次不等式的解法,考查了推理能力和计算能力,属于中档题.

练习册系列答案
相关题目
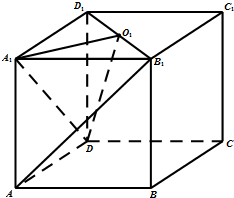 已知长方体ABCD-A1B1C1D1,点O1为B1D1的中点.
已知长方体ABCD-A1B1C1D1,点O1为B1D1的中点.
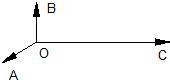 如图,平面内有三个向量
如图,平面内有三个向量