题目内容

正方体ABCD-A1B1C1D1的棱长为1，P是线段A1B上的一点，则AP+D1P的最小值是
 
．
考点：多面体和旋转体表面上的最短距离问题
专题：空间位置关系与距离
分析：把对角面A1C绕A1B旋转至A1BC′D1′，使其与△AA1B在同一平面上，连接AD1′并求出，就是最小值．
解答： 解：如图所示，把对角面A1C绕A1B旋转至A1BC′D1′，
使其与△AA1B在同一平面上，连接AD1′，
则AD1′=
1+1-2×1×1×cos135°
=
2-
2
为所求的最小值．
故答案为：
2-
2
．
点评：本题考查棱柱的结构特征，考查计算能力，空间想象能力，解决此类问题常通过转化，转化为在同一平面内两点之间的距离问题．
练习册系列答案
相关题目
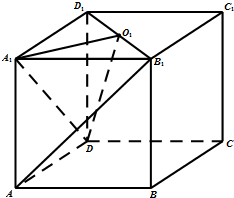已知长方体ABCD-A1B1C1D1，点O1为B1D1的中点．
（1）求证：AB1∥面A1O1D；
（2）若AB=
2
3
AA1，试问在线段BB1上是否存在点E使得A1C⊥AE，若存在求出
BE
BB1
，若不存在，说明理由．
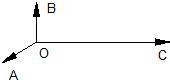如图，平面内有三个向量
OA
，
OB
，
OC
，其中
OA
与
OB
的夹角为120°，
OA
与
OC
的夹角为150°，且|
OA
|=|
OB
|=1，|
OC
|=2
3
．若
OC
=λ
OA
+μ
OB
（λ，μ∈R），则λ+μ的值为
 
．
若函数y=|ln（x-1）|的图象与函数y=ax-3a的图象有两个不同的交点，则实数a的取值范围为
 
．
圆心为C（-1，2），且与x轴相切的圆的标准方程为
 
．
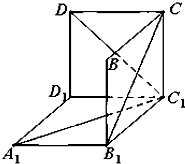如图是从上下底面处在水平状态下的棱长为a的正方体ABCD-A1B1C1D1中分离出来的．有如下结论：
①∠DC1D1在图中的度数和它表示的角的真实度数都是45°；
②∠A1C1D=∠A1C1D1+∠D1C1D；
③A1C1与BC1所成的角是30°；
④若BC=m，则用图示中这样一个装置盛水，最多能盛
1
6
m3的水．
其中正确的结论是
 
（请填上你所有认为正确结论的序号）．
若an=2n2+λn+3（其中λ为实常数），n∈N*，且数列{an}为单调递增数列，则实数λ的取值范围为
 
．
不论m取什么实数，直线（2m-1）x+（m+3）y-（m-11）=0都经过一个定点，则这个定点为
 
．
在平面直角坐标系xOy中，已知向量
a
=（1，0），
b
=（2，1）．若向量
a
+3
b
与k
a
-21
b
共线，则实数k的值为
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网