题目内容
给出下面几个命题:
①复平面内坐标原点就是实轴与虚轴的交点.
②设f(x)=ax3+3x2+2,若f′(-1)=4,则a的值等于
.
③某射手每次射击击中目标的概率是0.8,这名手在10次射击中恰有8次命中的概率约为0.30.
④若f(x)=log2x,则f′(x)=
.
其中假命题的序号是 .
①复平面内坐标原点就是实轴与虚轴的交点.
②设f(x)=ax3+3x2+2,若f′(-1)=4,则a的值等于
| 10 |
| 3 |
③某射手每次射击击中目标的概率是0.8,这名手在10次射击中恰有8次命中的概率约为0.30.
④若f(x)=log2x,则f′(x)=
| 1 |
| 2lnx |
其中假命题的序号是
考点:命题的真假判断与应用
专题:阅读型
分析:本题考查的知识点是:判断命题真假;比较综合的考查了复数、导数及概率的一些性质,我们可以根据复数、导数及概率的性质对四个结论逐一进行判断,可以得到正确的结论.
解答:
解:由于虚轴不包括原点,故①不正确;
由f′(x)=3ax2+6x得,f′(-1)=3a-6=4;所以a=
.故②正确.
p
0.880.22≈0.302;故③正确.
由(lo
)′=
,则f′(x)=
,故④不正确.
故答案为:①④.
由f′(x)=3ax2+6x得,f′(-1)=3a-6=4;所以a=
| 10 |
| 3 |
p
| =c | 2 10 |
由(lo
| g | x a |
| 1 |
| xlna |
| 1 |
| xln2 |
故答案为:①④.
点评:本题总结了高中易错的知识点:复平面内虚轴不包括原点;同时考查了学生对导数公式与运算的记忆与应用及概率的求法.综合性较强.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

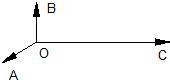 如图,平面内有三个向量
如图,平面内有三个向量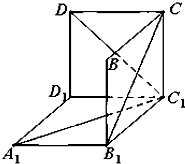 如图是从上下底面处在水平状态下的棱长为a的正方体ABCD-A1B1C1D1中分离出来的.有如下结论:
如图是从上下底面处在水平状态下的棱长为a的正方体ABCD-A1B1C1D1中分离出来的.有如下结论: