题目内容
若当P(m,n)为圆x2+(y-1)2=1上任意一点时,等式m+n+c=0恒成立,则c的取值范围是( )
A、-1-
| ||||
B、
| ||||
C、c≤-
| ||||
D、c≥
|
考点:圆的标准方程
专题:直线与圆
分析:令m=cosθ,n=1+sinθ,由等式m+n+c=0 可得c=-m-n=-
sin(θ+
)-1,再根据正弦函数的值域求得c的范围.
| 2 |
| π |
| 4 |
解答:
解:由题意可得m2+(n-1)2=1,令m=cosθ,n=1+sinθ,
由等式m+n+c=0 可得c=-m-n=-cosθ-sinθ-1=-
sin(θ+
)-1,
再由-1≤sin(θ+
)≤1,可得-
-1≤c≤
-1,
故选:A.
由等式m+n+c=0 可得c=-m-n=-cosθ-sinθ-1=-
| 2 |
| π |
| 4 |
再由-1≤sin(θ+
| π |
| 4 |
| 2 |
| 2 |
故选:A.
点评:本题主要考查圆的标准方程,三角恒等变换,正弦函数的值域,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
在△ABC中,若c2-ab=a2+b2,则∠C=( )
| A、60° | B、90° |
| C、120° | D、150° |
 如图网格中的图形为某个多面体的三视图,每个小正方形的边长为1,则该多面体的外接圆的表面积为( )
如图网格中的图形为某个多面体的三视图,每个小正方形的边长为1,则该多面体的外接圆的表面积为( )| A、3π | ||
B、32
| ||
| C、48π | ||
| D、192π |
已知向量
=(cosθ,sinθ),θ∈(
,π),
=(0,-1),则
与
的夹角等于( )
| a |
| π |
| 2 |
| b |
| a |
| b |
A、θ-
| ||
B、
| ||
C、
| ||
| D、θ |
如果执行如图所示的程序框图,输入正整数N(N≥2)和实数a1,a2,…,an,输出A,B,则( )
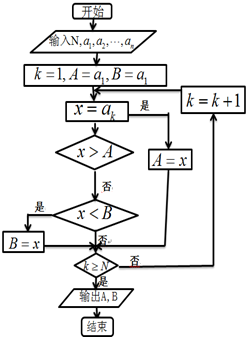

| A、A和B分别是a1,a2,…,an中最小的数和最大的数 | ||
| B、A和B分别是a1,a2,…,an中最大的数和最小的数 | ||
C、
| ||
| D、A+B为a1,a2,…,an的和 |
在10个形状大小均相同的球中有6个红球和4个白球,不放回地依次摸出2个球,在第1次摸出红球的条件下,第2次也摸到红球的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
已知α,β∈R,设p:α>β,设q:α-sinβcosα>β-sinαcosβ,则p是q的( )
| A、充分必要条件 |
| B、充分不必要条件 |
| C、必要不充分条件 |
| D、既不充分也不必要条件 |